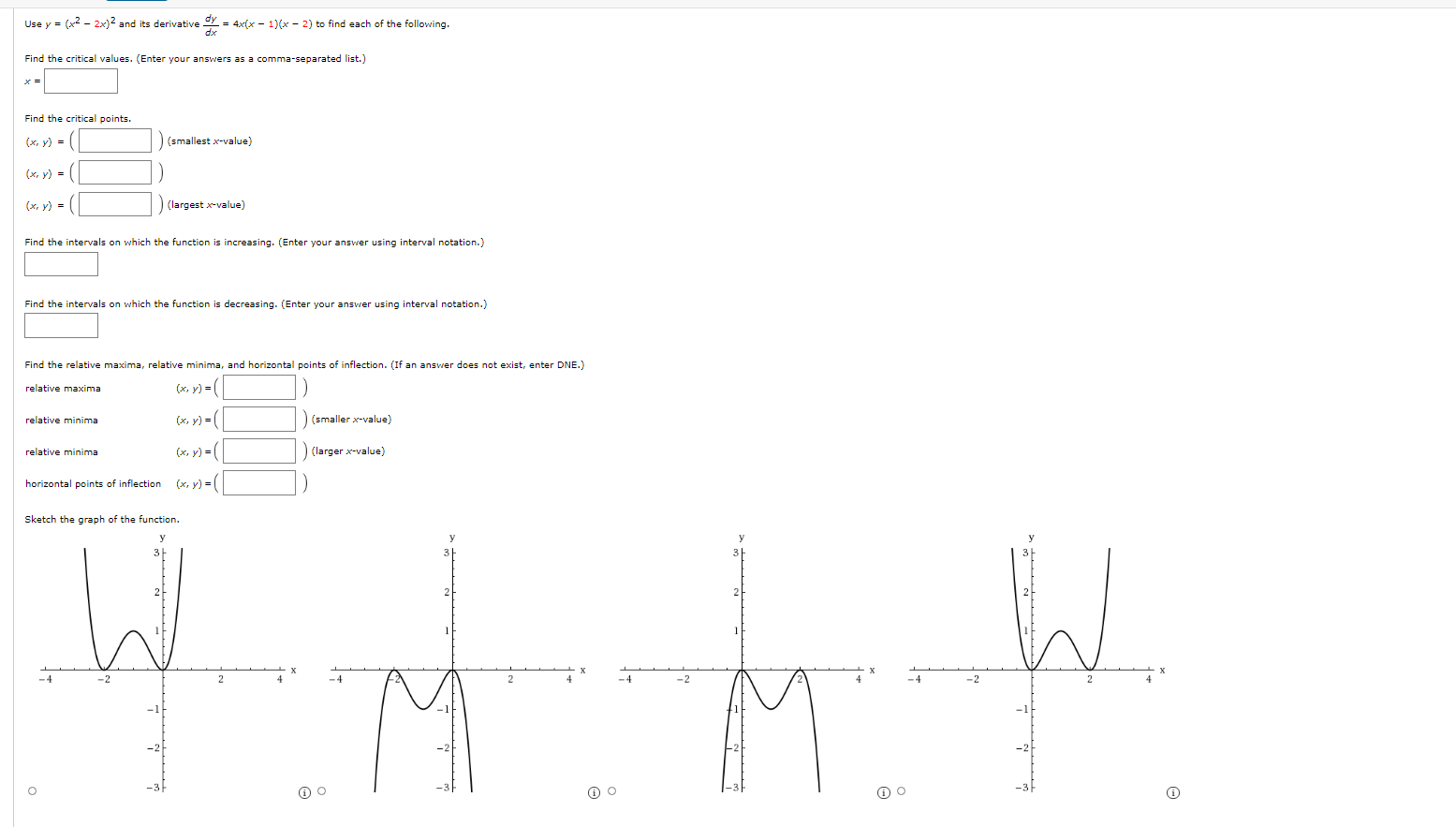
Question: Use y = ( x 2 ?2 x ) 2 and its derivative dy dx = 4 x ( x ?1)( x ?2) to find
Usey= (x2?2x)2
and its derivativedy
dx
= 4x(x?1)(x?2)
to find each of the following.
Find the critical values. (Enter your answers as a comma-separated list.)
x=
Find the critical points.
(x,y)=(smallestx-value)(x,y)=(x,y)=(largestx-value)
Find the intervals on which the function is increasing. (Enter your answer using interval notation.)
Find the intervals on which the function is decreasing. (Enter your answer using interval notation.)
Find the relative maxima, relative minima, and horizontal points of inflection. (If an answer does not exist, enter DNE.)
relative maxima(x,y)
=
relative minima(x,y)
=
(smallerx-value)relative minima(x,y)
=
(largerx-value)horizontal points of inflection(x,y)
=
Sketch the graph of the function.
Thexy-coordinate plane is given. The curve enters the window in the second quadrant, goes down and right becoming less steep, changes direction at the point(?2, 0),goes up and right becoming more steep, passes through the approximate point(?1.58, 0.44),goes up and right becoming less steep, changes direction at the point(?1, 1),goes down and right becoming more steep, passes through the approximate point(?0.42, 0.44),goes down and right becoming less steep, changes direction at the origin, goes up and right becoming more steep, and exits the window in the first quadrant.
Thexy-coordinate plane is given. The curve enters the window in the third quadrant, goes up and right becoming less steep, changes direction at the point(?2, 0),goes down and right becoming more steep, passes through the approximate point(?1.58,?0.44),goes down and right becoming less steep, changes direction at the point(?1,?1),goes up and right becoming more steep, passes through the approximate point(?0.42,?0.44),goes up and right becoming less steep, changes direction at the origin, goes down and right becoming more steep, and exits the window in the fourth quadrant.
Thexy-coordinate plane is given. The curve enters the window in the third quadrant, goes up and right becoming less steep, changes direction at the origin, goes down and right becoming more steep, passes through the approximate point(0.42,?0.44),goes down and right becoming less steep, changes direction at the point(1,?1),goes up and right becoming more steep, passes through the approximate point(1.58,?0.44),goes up and right becoming less steep, changes direction at the point(2, 0),goes down and right becoming more steep, and exits the window in the fourth quadrant.
Thexy-coordinate plane is given. The curve enters the window in the second quadrant, goes down and right becoming less steep, changes direction at the origin, goes up and right becoming more steep, passes through the approximate point(0.42, 0.44),goes up and right becoming less steep, changes direction at the point(1, 1),goes down and right becoming more steep, passes through the approximate point(1.58, 0.44),goes down and right becoming less steep, changes direction at the point(2, 0),goes up and right becoming more steep, and exits the window in the first quadrant.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts