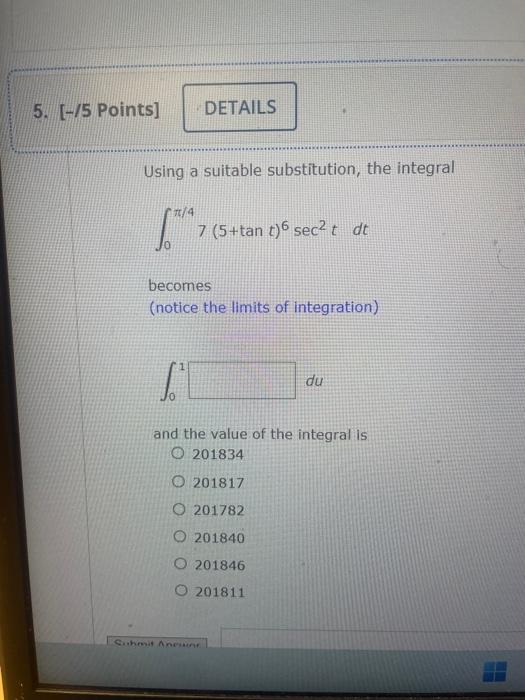
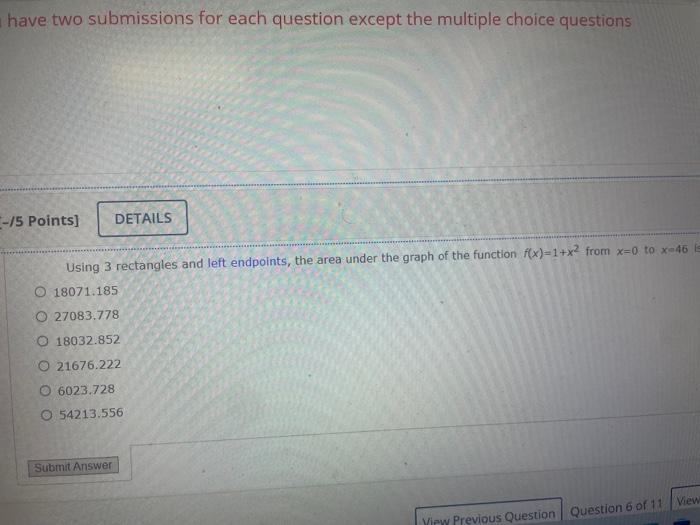
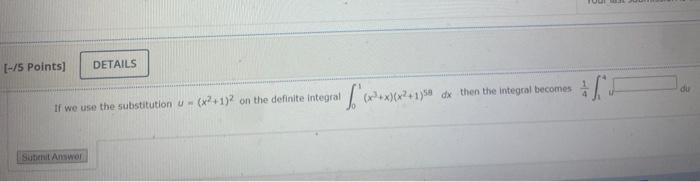
Using a suitable substitution, the integral 0/47(5+tant)6sec2tdt becomes (notice the limits of integration) and the value of the integral is 201834 201817 201782 201840 201846 201811 have two submissions for each question except the multiple choice questions Using 3 rectangles and left endpoints, the area under the graph of the function f(x)=1+x2 from x=0 to x=46 18071.185 27083.778 18032.852 21676.222 6023.728 54213.556 If we use the substitution u=(x2+1)2 on the definite integral 01(x3+x)(x2+1)59dx then the integral becomes 4114