Using MATLAB*

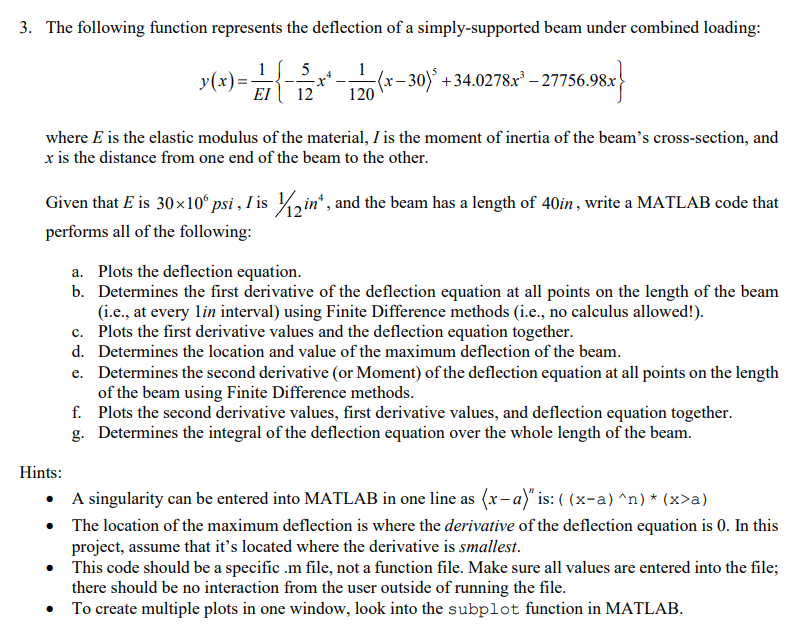
3. The following function represents the deflection of a simply-supported beam under combined loading: y(x)=EI1{125x41201x305+34.0278x327756.98x} where E is the elastic modulus of the material, I is the moment of inertia of the beam's cross-section, and x is the distance from one end of the beam to the other. Given that E is 30106psi,I is 1/12in4, and the beam has a length of 40in, write a MATLAB code that performs all of the following: a. Plots the deflection equation. b. Determines the first derivative of the deflection equation at all points on the length of the beam (i.e., at every 1 in interval) using Finite Difference methods (i.e., no calculus allowed!). c. Plots the first derivative values and the deflection equation together. d. Determines the location and value of the maximum deflection of the beam. e. Determines the second derivative (or Moment) of the deflection equation at all points on the length of the beam using Finite Difference methods. f. Plots the second derivative values, first derivative values, and deflection equation together. g. Determines the integral of the deflection equation over the whole length of the beam. Hints: - A singularity can be entered into MATLAB in one line as xan is: ((xa)n)(x>a) - The location of the maximum deflection is where the derivative of the deflection equation is 0 . In this project, assume that it's located where the derivative is smallest. - This code should be a specific .m file, not a function file. Make sure all values are entered into the file; there should be no interaction from the user outside of running the file. - To create multiple plots in one window, look into the subplot function in MATLAB