Using Matlab to write a user-defined function that solves for a root of a nonlinear equation f(x)=0 using the bisection method. Name the function Xs = BisectionRoot(fun,a,b). The output argument Xs is the solution. The input argument Fun is the name for the function that calculates f(x) for a given x, and a and b are two points that bracket the root. The itreations should stop when the tolerance in f(x) is smaller than 0.000001. The program should check that a and b are on opposite sides of the soultion. If not, the program should stop and display an error message.

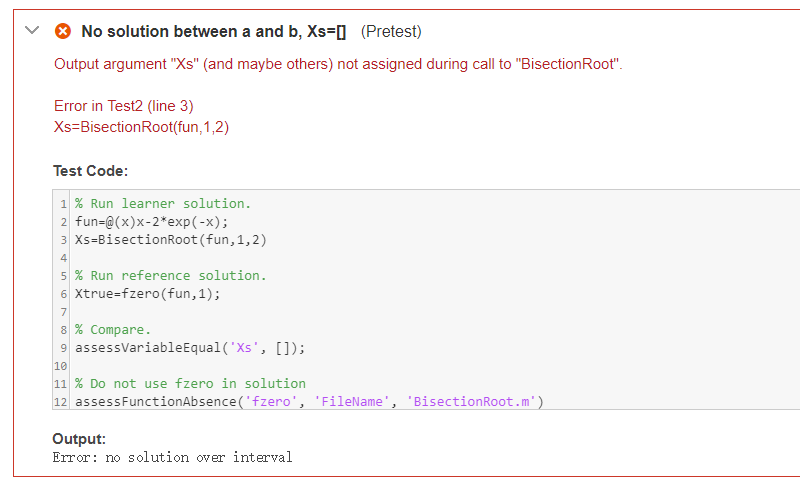
My code is almost correct, but it still has some problems. I just need someone help me fix it.

function Xs=BisectionRoot(fun,a,b)

% fun is an anonymous function

% a and b are the range over which the solution Xs exists

iter=0;

maxiter=1000; % quit after 1000 iterations

tol=1e-6; % convergence criterion

fa=fun(a);

fb=fun(b);

if fa*fb>0

disp('Error: no solution over interval')

else

toli=tol+1; % ensure we enter loop

while toli>tol

Xs=(a+b)/2; % Bisection

% xNS=(a*fb-b*fa)/(fb-fa); % Regula Falsi

fxNS=fun(Xs);

fprintf('iter %4i, x=%6.5f, f(x)=%9.2e ',iter,Xs,fxNS)

if fxNS==0

disp('exact solution found')

break

elseif fa*fxNS

toli=abs(b-Xs); % correction

b=Xs;

fb=fxNS;

elseif fa*fxNS>0

toli=abs(a-Xs); % correction

a=Xs;

fa=fxNS;

else

disp('no solution over interval');

break

iter=iter+1;

if iter>maxiter

fprintf('did not converge in %i iterations ',iter)

break

end

end

fprintf('solution is x = %f ',Xs)

end

end