Using Matlab..."put the outputs and codes "... the functions you need are under the problem:

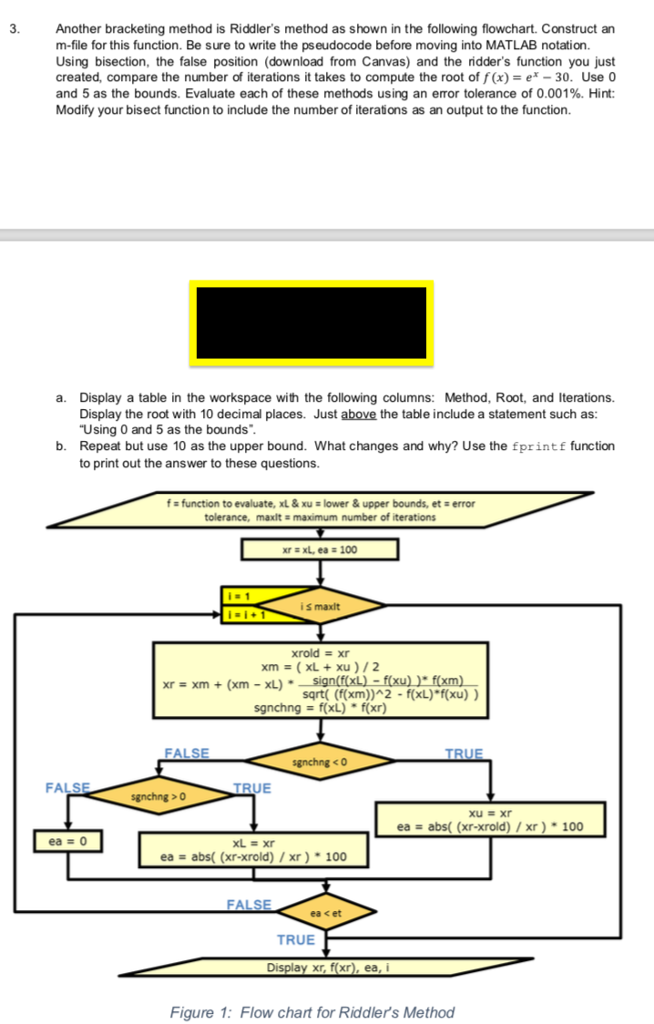
1- falsep

function [xr, fx, ea, i] = falsep(f,xL,xu,et,maxIt)

% falsep: false position root locator that finds roots between xL and xu

% Inputs:

% f - function to be evaluated

% xL, xu - lower and upper bounds, respectively

% et - maximum allowable error (default 0.0001%)

% maxIt - maximum number of iterations (default 50)

% Outputs:

% xr - root found

% fx - function value at root

% ea - approximate relative error (%)

% i - number of iterations necessary to obtain solution

if nargin

test = f(xL)*f(xu);

if test>0,error('No sign change between f(xL) and f(xu)'),end

if nargin

if nargin

xr = xL; ea = 100;

for i = 1:maxIt

xrold = xr;

xr = xu-f(xu)*(xL-xu)/(f(xL)-f(xu));

sgnchng = f(xL)*f(xr);

if sgnchng

xu = xr;

ea = abs((xr-xrold)/xr)*100;

elseif sgnchng > 0

xL = xr;

ea = abs((xr-xrold)/xr)*100;

else

ea = 0;

end

if ea

end

fx = f(xr);

2- bisect

function [xr,fx,ea,i] =bisect(f,xL,xu,et)

% bisect: bisection root locator that finds roots between xL and xu

% Inputs:

% f - function to be evalauted

% xL,xu - lower and upper bounds, respectively

% et - maximum allowable error(default 0.0001%)

% Outputs:

% xr-root found

% fc - function value at root

% ea - approximate relative error(%)

% i - number of iterations completed

%

%

if nargin

test=f(xL)*f(xu);

if test>0, error('No sign change between f(xL) and f(xu)'),end

if nargin

xr=xL;

ea=100;

for i=1:50

xrold =xr;

xr = (xL+xu)/2;

sgnchng=f(xL)*f(xr);

if sgnchng

xu=xr;

ea=abs((xr-xrold)/xr)*100;

elseif sgnchng>0

xL=xr;

ea=abs((xr-xrold)/xr)*100;

else

ea=0;

end

if ea

end

fx=f(xr);

3. Another bracketing method is Riddler's method as shown in the following flowchart. Construct an m-file for this function. Be sure to write the pseudocode before moving into MATLAB notation. Using bisection, the false position (download from Canvas) and the ridder's function you just created, compare the number of iterations it takes to compute the root of f(x) = ex-30. Use 0 and 5 as the bounds. Evaluate each of these methods using an error tolerance of 0.001%. Hint: Modify your bisect function to include the number of iteratons as an output to the function. a. Display a table in the workspace with the following columns: Method, Root, and Iterations. Display the root with 10 decimal places. Just above the table include a statement such as: Using O and 5 as the bounds Repeat but use 10 as the upper bound. What changes and why? Use the fprintf function to print out the answer to these questions. b. function to evaluate, xL & xu lower & upper bounds, eta error tolerance, maxit maximum number of iterations xr a xL. ea 100 i S maxit xm = ( xL + xu ) / 2 sqrt( (f(xm))2-f(xL) f(xu)) sgnchng = f(xl) * f(xr) FALSE TRUF FALSE sgnchng>o ea abs( (xr-xrold) / xr ) * 100 ea abs( (xr-mold) / xr ) * 100 FALSE ea o ea abs( (xr-xrold) / xr ) * 100 ea abs( (xr-mold) / xr ) * 100 FALSE ea