_{using minitab}

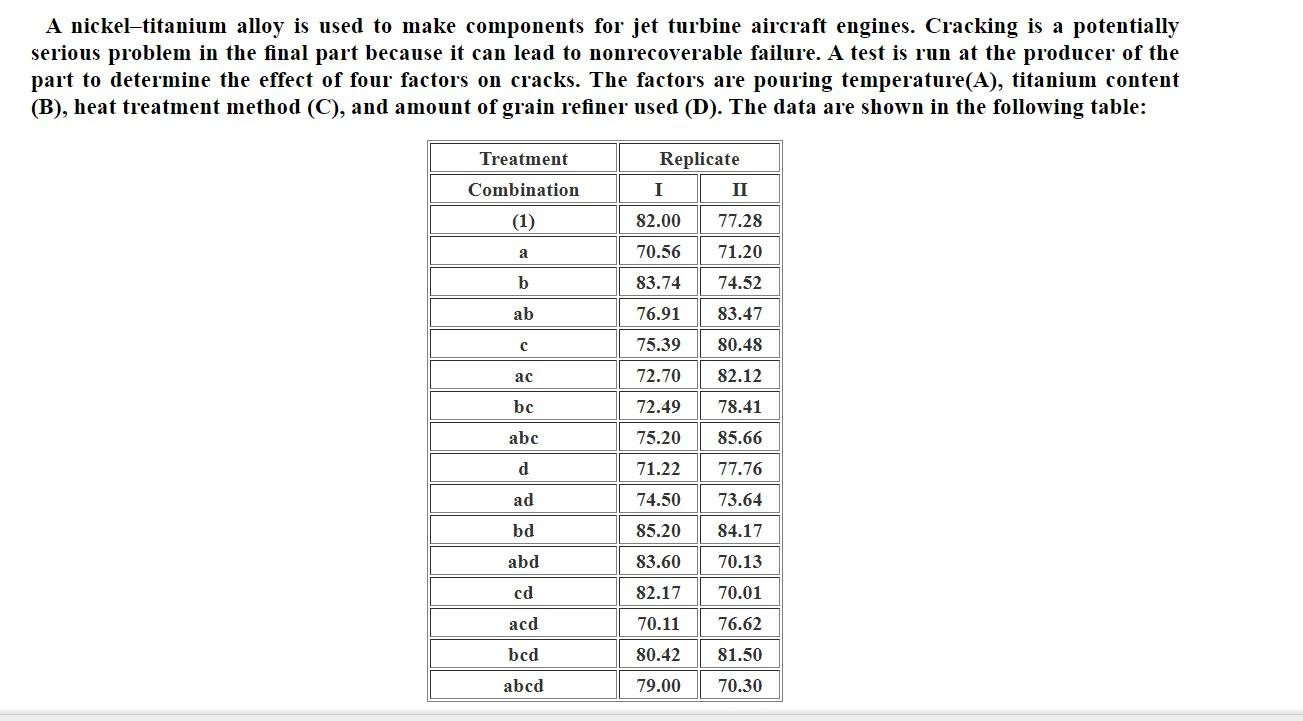
A nickel-titanium alloy is used to make components for jet turbine aircraft engines. Cracking is a potentially serious problem in the final part because it can lead to nonrecoverable failure. A test is run at the producer of the part to determine the effect of four factors on cracks. The factors are pouring temperature(A), titanium content (B), heat treatment method (C), and amount of grain refiner used (D). The data are shown in the following table: Treatment Replicate I II Combination (1) 77.28 82.00 70.56 a 71.20 b 74.52 83.74 76.91 ab 83.47 75.39 80.48 ac 72.70 82.12 bc 72.49 78.41 abc 75.20 85.66 d 71.22 77.76 ad 74.50 73.64 bd 85.20 84.17 abd 83.60 70.13 cd 82.17 70.01 acd 70.11 76.62 bcd 80.42 81.50 abcd 79.00 70.30 a. Estimate the factor effects. Which factor do effects appear to be large? b. Conduct an analysis of variance. Do any factors affect cracking? Use a =0.1. c. Write down a regression model that can be used to predict crack length as a function of the significant main effects and interactions you have identified in part (b). d. Analyze the residuals from this experiment? e. Suppose that only 16 runs could be made on a single day, so each replicate was treated as a block. Analyze the experiment and draw conclusions. f. Suppose that only a one-half fraction of the design could be run. Construct the design (table of observation for the new design) and perform the analysis, using the data from replicate II. Use a=0.5 (Hint: if it is required you have to find the alternate) A nickel-titanium alloy is used to make components for jet turbine aircraft engines. Cracking is a potentially serious problem in the final part because it can lead to nonrecoverable failure. A test is run at the producer of the part to determine the effect of four factors on cracks. The factors are pouring temperature(A), titanium content (B), heat treatment method (C), and amount of grain refiner used (D). The data are shown in the following table: Treatment Replicate I II Combination (1) 77.28 82.00 70.56 a 71.20 b 74.52 83.74 76.91 ab 83.47 75.39 80.48 ac 72.70 82.12 bc 72.49 78.41 abc 75.20 85.66 d 71.22 77.76 ad 74.50 73.64 bd 85.20 84.17 abd 83.60 70.13 cd 82.17 70.01 acd 70.11 76.62 bcd 80.42 81.50 abcd 79.00 70.30 a. Estimate the factor effects. Which factor do effects appear to be large? b. Conduct an analysis of variance. Do any factors affect cracking? Use a =0.1. c. Write down a regression model that can be used to predict crack length as a function of the significant main effects and interactions you have identified in part (b). d. Analyze the residuals from this experiment? e. Suppose that only 16 runs could be made on a single day, so each replicate was treated as a block. Analyze the experiment and draw conclusions. f. Suppose that only a one-half fraction of the design could be run. Construct the design (table of observation for the new design) and perform the analysis, using the data from replicate II. Use a=0.5 (Hint: if it is required you have to find the alternate)