Using Pumping Lemma one can show the language L= {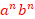 | n N } is not regular. This is done by way of contradiction. We assume L is regular. Since L is infinite, Pumping Lemma applies. We then consider the string 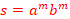where 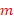is the number of states of the DFA that recognizes L. Since the length of 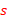is bigger than 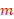, by Pumping Lemma, there exists strings 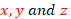such that 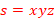, , 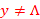and 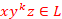for all . If 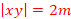then the first repeated state on the acceptance path must be a final state. Why?