Using Pyhton to answer the question, show the code and plots. Thank you so much!

Date	United States
12/30/2007	2278
1/6/2008	2199
1/13/2008	2230
1/20/2008	2921
1/27/2008	3880
2/3/2008	4928
2/10/2008	5352
2/17/2008	5805
2/24/2008	5050
3/2/2008	4059
3/9/2008	3229
3/16/2008	2592
3/23/2008	2172
3/30/2008	1776
4/6/2008	1508
4/13/2008	1331
4/20/2008	1180
4/27/2008	1046
5/4/2008	947
5/11/2008	922
5/18/2008	873
5/25/2008	828
6/1/2008	770
6/8/2008	727
6/15/2008	713
6/22/2008	662
6/29/2008	646
7/6/2008	665
7/13/2008	638
7/20/2008	627
7/27/2008	634
8/3/2008	648
8/10/2008	684
8/17/2008	710
8/24/2008	771
8/31/2008	903
9/7/2008	1009
9/14/2008	1114
9/21/2008	1221
9/28/2008	1275
10/5/2008	1334
10/12/2008	1404
10/19/2008	1543
10/26/2008	1659
11/2/2008	1747
11/9/2008	1953
11/16/2008	2194
11/23/2008	1969
11/30/2008	2045
12/7/2008	1938
12/14/2008	1870
12/21/2008	1942
12/28/2008	2100

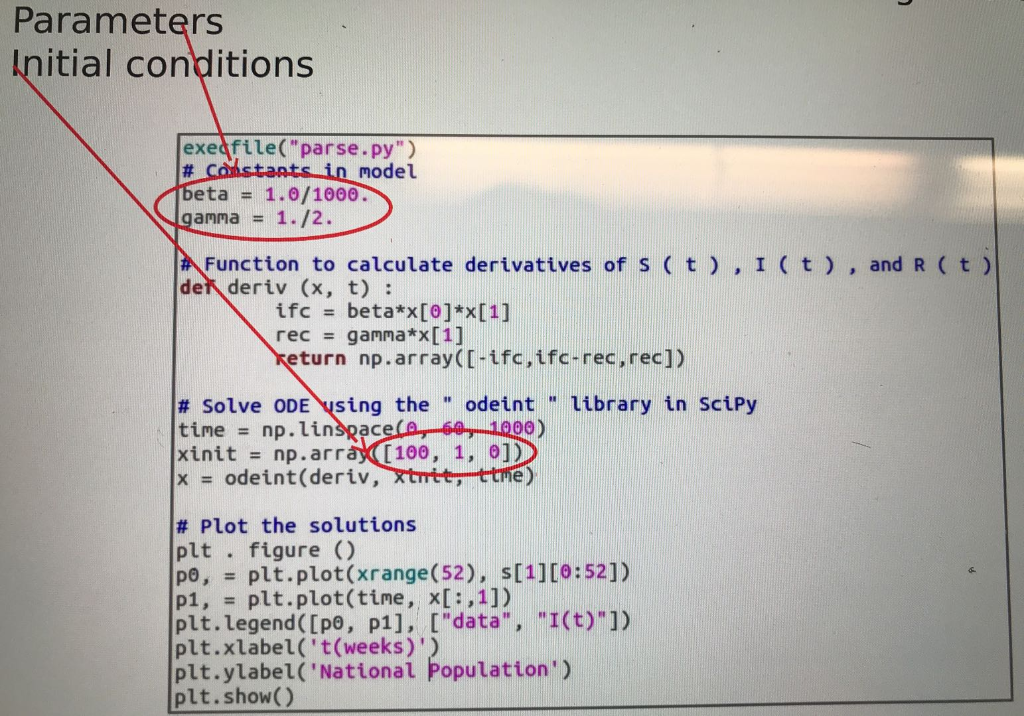
Parameters Initial conditions exedfile("parse.py") # Constants in model beta = 1.0/1000. gamma = 1./2. # Function to calculate derivatives of s ( t), 1(t), and R (t) de deriv (x, t) : ifc = beta*x[@]*x[1] rec = gamma*x[1] keturn np.array([-ifc, ifc-rec, rec]). # Solve ODE using the " odeint " library in Scipy time = np.linspace(a, 60, 1000) xinit = np.array(100, 1, 0]) x = odeint(deriv, xtutt, ttme) # Plot the solutions plt . figure () po, = plt.plot(xrange(52), s[1][0:52]) pi, = plt.plot(time, x[:,1]) plt.legend([po, p1], ["data", "I(t)"]) plt.xlabel('t(weeks)') plt.ylabel('National population) plt.show() Parameters Initial conditions exedfile("parse.py") # Constants in model beta = 1.0/1000. gamma = 1./2. # Function to calculate derivatives of s ( t), 1(t), and R (t) de deriv (x, t) : ifc = beta*x[@]*x[1] rec = gamma*x[1] keturn np.array([-ifc, ifc-rec, rec]). # Solve ODE using the " odeint " library in Scipy time = np.linspace(a, 60, 1000) xinit = np.array(100, 1, 0]) x = odeint(deriv, xtutt, ttme) # Plot the solutions plt . figure () po, = plt.plot(xrange(52), s[1][0:52]) pi, = plt.plot(time, x[:,1]) plt.legend([po, p1], ["data", "I(t)"]) plt.xlabel('t(weeks)') plt.ylabel('National population) plt.show()