Using Python.

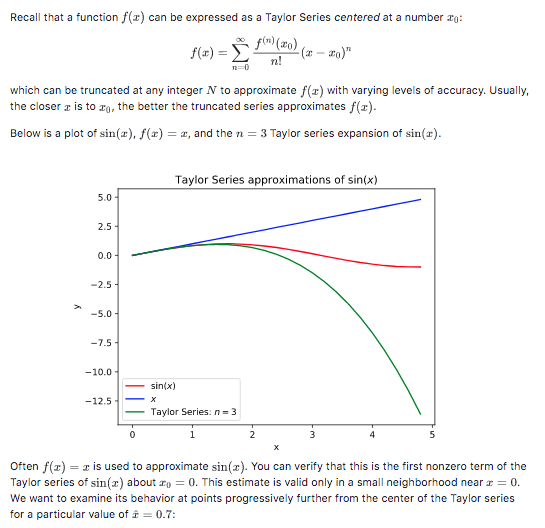
Recall that a function f(x) can be expressed as a Taylor Series centered at a number : f(x) = f (PO) (2 - 4a)" which can be truncated at any integer N to approximate f(2) with varying levels of accuracy. Usually, the closer is to 3o, the better the truncated series approximates f(x). Below is a plot of sin(x), f(x) = x, and the n = 3 Taylor series expansion of sin(a). Taylor Series approximations of sin(x) in bio in - 125 sin(x) x Taylor Series: n=3 - Often f(x) = x is used to approximate sin(:). You can verify that this is the first nonzero term of the Taylor series of sin(s) about 10 = 0. This estimate is valid only in a small neighborhood near x = 0. We want to examine its behavior at points progressively further from the center of the Taylor series for a particular value of t = 0.7: Calculate the n=1 and n = 3 Taylor series expansions of sin(a) about to = 0 evaluated at 2. Calculate the n = 3 Taylor series expansion of sin() about 20 = evaluated at e. Calculate the true value of sin(i). Use this value to calculate the relative errors of the approximations. Save the results in err_2_1, err_0_3, and err_pi4_3. Remember that the formula for relative error is owner. Your code snippet should define the following variables: Name Type floating point number floating point number floating point number Description error when x 0 = 0 and n=1 error when x 0 = 0 and n=3 error when x 0 = pi/4 and n=3 err 3 3 lerr pi4 3