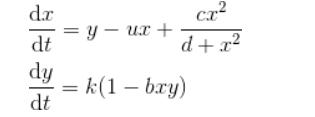
t	0	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360
x	0	3.05	2.04	0.34	0.63	0.95	1.60	2.27	1.60	0.44	0.75	1.13	1.82	2.20	0.56	0.54	0.86	1.32	2.18
y	1	0.28	0.18	0.32	0.38	0.46	0.35	0.22	0.20	0.32	0.40	0.39	0.31	0.22	0.22	0.33	0.40	0.37	0.27

 

 

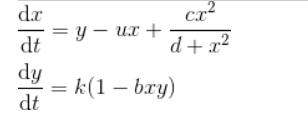
t	0	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360
x	0	3.05	2.04	0.34	0.63	0.95	1.60	2.27	1.60	0.44	0.75	1.13	1.82	2.20	0.56	0.54	0.86	1.32	2.18
y	1	0.28	0.18	0.32	0.38	0.46	0.35	0.22	0.20	0.32	0.40	0.39	0.31	0.22	0.22	0.33	0.40	0.37	0.27

(b) Use Matlab's lsqcurvefit instead of fminsearch to answer the same question as (a).
 

Consider the following biochemical oscillator model dx cx (1) dt d+x == k (1-bay) dt where x and y are state variables(say protein concentrations) and , c, d, k and b are positive constants. If you are provided time series data for the state variables x = x(t) and y = y(t), then it is mathematically possible to compute estimates for the unknown parameters by minimizing the distance between model predicted values and the data points for each time points. Table 1: Artificial time series data for the model given in Eq.(1) |t0| 20 | 40 | 60 80 100 120 140 160 180 200 220 240 200 250 300-320 340 x 360 0 3.05 2.04 0.34 0.63 0.95 1.60 2.27 1.60 0.44 0.75 1.13 1.82 2.20 0.56 0.54 0.86 1.32 2.18 y 1 0.28 0.18 0.32 0.38 0.46 0.35 0.22 0.20 0.32 0.40 0.39 0.31 0.22 0.22 0.33 0.40 0.37 0.27 1