Using the Rejection Method in section 5.2.4, Algorithm 5.4, code (preferably in Python) a program to generate random variables X with distribution determined by the density function f(x) = 1/3 (x-1)2 on the interval [0,3].

Write a subroutine that implements steps 1,2,3,4 of Algorithm 5.4, then call it at least 10,000 times. Make a table of values 0, 0.1, 0.2, ... 2.8, 2.9 and keep a running tally of the number of variables that fall within each interval.

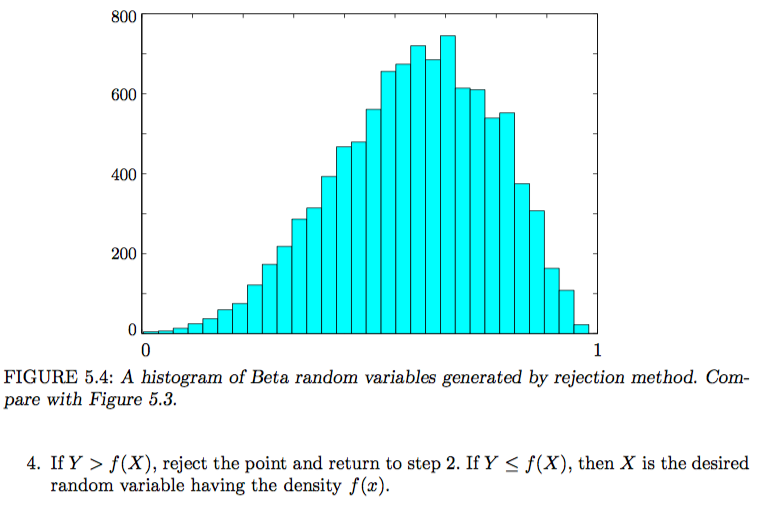
At the end of the program, print out a histogram showing how the values accumulated. It should look like the graph presented in class.

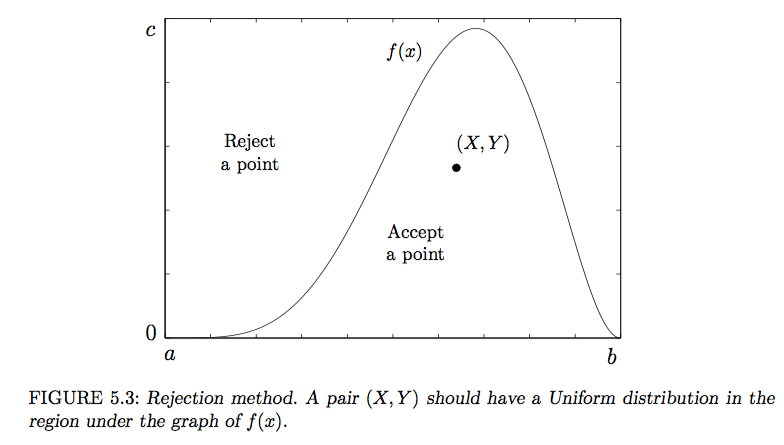
5.2.4 Rejection method Besides a good computer, one thing is needed to generate continuous variables using the inverse transform method of Section 5.2.3. It is a reasonably simple form of the cdf F(x) that allows direct computation of XF When F(x) has a complicated form but a density f() is available, random variables with this density can be generated by rejection method. Consider a point (X, Y) chosen at random from under the graph of density f(x), as shown in Figure 5.3. What is the distribution of X, its first coordinate? Theorem 3 Let a pair (X, Y) have Uniform distribution over the region for some density function f. Then f is the density of X. 5.2.4 Rejection method Besides a good computer, one thing is needed to generate continuous variables using the inverse transform method of Section 5.2.3. It is a reasonably simple form of the cdf F(x) that allows direct computation of XF When F(x) has a complicated form but a density f() is available, random variables with this density can be generated by rejection method. Consider a point (X, Y) chosen at random from under the graph of density f(x), as shown in Figure 5.3. What is the distribution of X, its first coordinate? Theorem 3 Let a pair (X, Y) have Uniform distribution over the region for some density function f. Then f is the density of X