$(!$v is used to represent the Boolean connective NOR$)$

NOR is the only Boolean connective operand that can be used $($DO NOT use or and not etc...$)$

Any stub with XXX needs to be filled out.

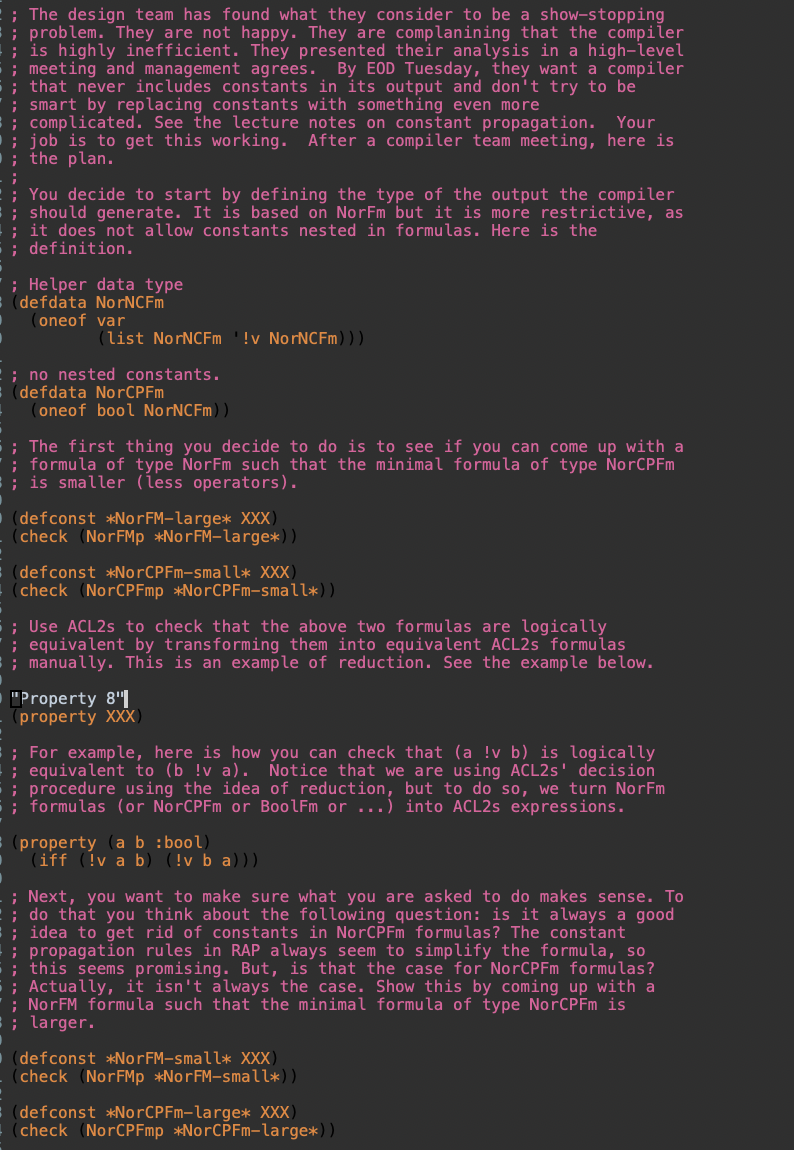
The design team has found what they consider to be a show$-$stopping

problem. They are not happy. They are complanining that the compiler

is highly inefficient. They presented their analysis in a high$-$level

meeting and management agrees. By EOD Tuesday, they want a compiler

that never includes constants in its output and don't try to be

smart by replacing constants with something even more

complicated. See the lecture notes on constant propagation. Your

job is to get this working. After a compiler team meeting, here is

the plan.

You decide to start by defining the type of the output the compiler

should generate. It is based on NorFm but it is more restrictive, as

it does not allow constants nested in formulas. Here is the

definition.

; Helper data type

$($defdata NorNCFm

$($oneof var

$($list NorNCFm $\text{'}!$v NorNCFm$)))$

; no nested constants.

$($defdata NorCPFm

$($oneof bool NorNCFm$))$

; The first thing you decide to do is to see if you can come up with a

; formula of type NorFm such that the minimal formula of type NorCPFm

; is smaller $($less operators$).$

$($defconst NorFM$-$large XXX$)$

$($check $($NorFMp NorFM$-$large$))$

$($defconst NorCPFm$-$small XXX$)$

$($check $($NorCPFmp NorCPFm$-$small$))$

; Use ACL$2$s to check that the above two formulas are logically

; equivalent by transforming them into equivalent ACL$2$s formulas

; manually. This is an example of reduction. See the example below.

#Property $8"\backslash$

$($property XXX$)$

; For example, here is how you can check that $($a $!$v b$)$ is logically

; equivalent to $($b $!$v a$).$ Notice that we are using ACL$2$s$\text{'}$ decision

; procedure using the idea of reduction, but to do so$,$ we turn NorFm

; formulas $($or NorCPFm or BoolFm or $...)$ into ACL$2$s expressions.

$($property $($a b :bool$)$

$($iff $(!$v a b$)(!$v b a$)))$

; Next, you want to make sure what you are asked to do makes sense. To

; do that you think about the following question: is it always a good

; idea to get rid of constants in NorCPFm formulas? The constant

; propagation rules in RAP always seem to simplify the formula, so

; this seems promising. But, is that the case for NorCPFm formulas?

; Actually, it isn't always the case. Show this by coming up with a

; NorFM formula such that the minimal formula of type NorCPFm is

; larger.

$($defconst NorFM$-$small XXX$)$

$($check $($NorFMp NorFM$-$small$))$

$($defconst NorCPFm$-$large XXX$)$

$($check $($NorCPFmp NorCPFm$-$large$))$