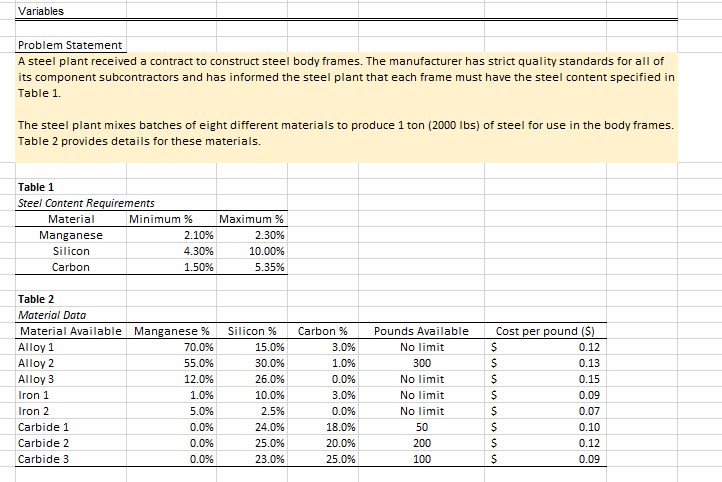
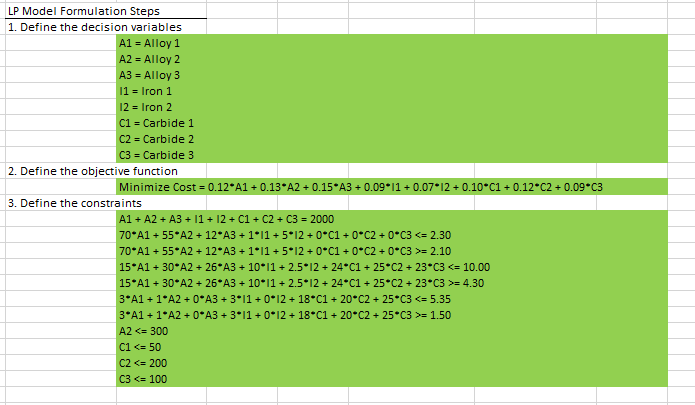
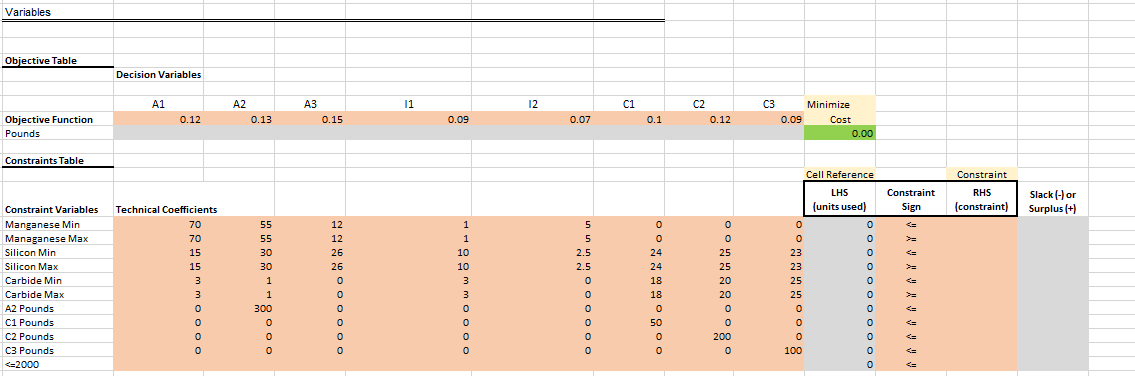
Variables Problem Statement A steel plant received a contract to construct steel body frames. The manufacturer has strict quality standards for all of its component subcontractors and has informed the steel plant that each frame must have the steel content specified in Table 1. The steel plant mixes batches of eight different materials to produce 1 ton (2000 lbs) of steel for use in the body frames. Table 2 provides details for these materials. Table 1 Steel Content Requirements Material Minimum % Maximum % Manganese 2.10% 2.30% Silicon 4.30% 10.00% Carbon 1.50% 5.35% Table 2 Material Data Material Available Manganese % Silicon % Carbon % Pounds Available Cost per pound ($) Alloy 1 70.0% 15.0% 3.0% No limit 0.12 Alloy 2 55.0% 30.0% 1.0% 300 0.13 Alloy 3 12.0% 26.0% 0.0% No limit 0.15 Iron 1 1.0% 10.0% 3.0% No limit 0.09 Iron 2 5.0% 2.5% 0.0% No limit 0.07 Carbide 1 0.0% 24.0% 18.0% 50 0.10 Carbide 2 0.0% 25.0% 20.0% 200 0.12 Carbide 3 0.0% 23.0% 25.0% 100 0.09LP Model Formulation Steps 1. Define the decision variables A1 = Alloy 1 A2 = Alloy 2 A3 = Alloy 3 11 = Iron 1 12 = Iron 2 C1 = Carbide 1 C2 = Carbide 2 C3 = Carbide 3 2. Define the objective function Minimize Cost = 0.12*A1 + 0.13*A2 + 0.15*A3 + 0.09*11 + 0.07*12 + 0.10*C1 + 0.12*C2 + 0.09*C3 3. Define the constraints A1 + A2 + A3 + 11 + 12 + C1 + C2 + 03 = 2000 70*A1 + 55*A2 + 12*A3 + 1*11 + 5*12 + 0*C1 + 0*C2 + 0*C3 = 2.10 15*A1 + 30*A2 + 26*A3 + 10*11 + 2.5*12 + 24*C1 + 25*C2 + 23*C3 = 4.30 3*A1 + 1"A2 + 0*A3 + 3*11 + 0*12 + 18*C1 + 20*C2 + 2503 = 1.50 A2