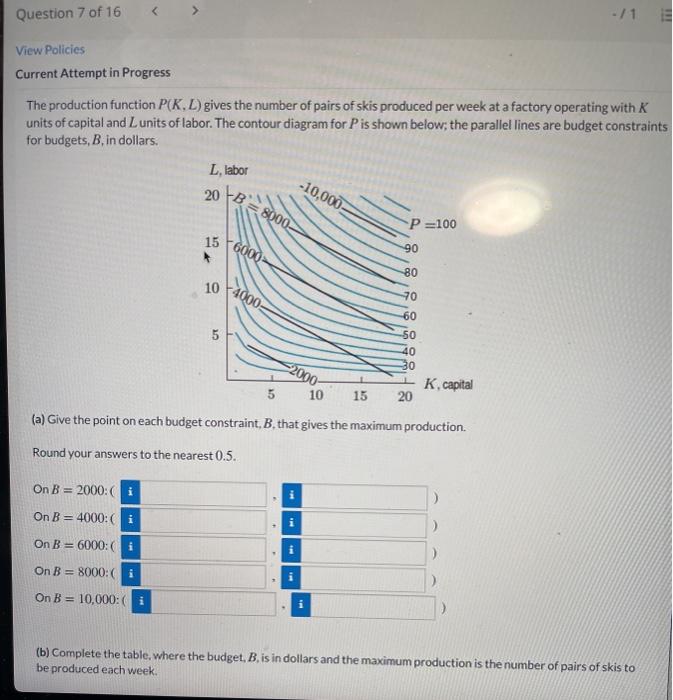
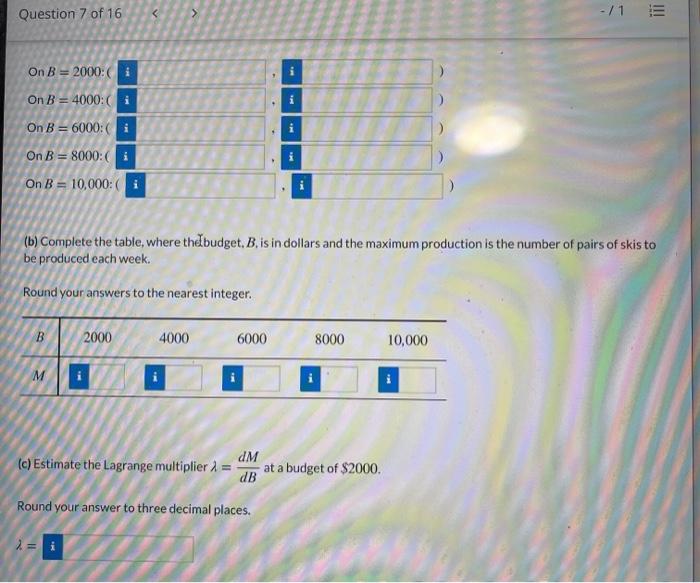
View Policies Current Attempt in Progress A company has the production function P(x,y), which gives the number of units that can be produced for given values of x and y: the cost function C (x,y) gives the cost of production for given values of x and y. (a) If the company wishes to maximize production at a cost of $60,000, what is the objective function? What is the constraint equation? What is the meaning of in this situation? The objective function is f = The constraint equation is represents the change in when is increased to (b) if instead the company wishes to minimize the costs at a fixed production level of 5000 units, what is the objective function? What is the constraint equation? What is the meaning of 2 in this situation? The objective function is f = The constraint equation is > II a represents the change in > when is increased to e Textbook and Media Save for Later View Policies Current Attempt in Progress You have set aside 28 hours to work on two class projects. You want to maximize your grade (measured in points), which depends on how you divide your time between the two projects. (a) What is the objective function for this optimization problem and what are its units? The objective function is your and the units are (b) What is the constraint? (c) Suppose you solve the problem by the method of Lagrange multipliers. What are the units for i? (d) What is the practical meaning of the statement i = 6? Enter the exact answers. Working hours instead of 28 hours will improve your grade by approximately points. Current Attempt in Progress A steel manufacturer can produce P(K.L) tons of steel using K units of capital and Lunits of labor, with production costs C (K, L) dollars. With a budget of $900,000, the maximum production is 10,000 tons, using $650,000 of capital and $250,000 of labor. The Lagrange multiplier is i = 0.10. (a) What is the objective function? (b) What is the constraint? V= (c) What are the units for ? (d) What is the practical meaning of the statement i = 0.10? Every extra dollar of budget maximal production by approximately i = 0.10 tons. Question 7 of 16 -11 View Policies Current Attempt in Progress The production function P(K. D) gives the number of pairs of skis produced per week at a factory operating with K units of capital and Lunits of labor. The contour diagram for P is shown below; the parallel lines are budget constraints for budgets, B in dollars. L, labor 20 te -10,000 8000 P=100 15 6000 90 80 10 4000 70 60 50 40 30 -2000 IK, capital 10 5 15 20 (a) Give the point on each budget constraint, B that gives the maximum production. Round your answers to the nearest 0.5. On B= 2000: i On B = 4000: i i On B = 6000: i i On B = 8000:( i On B = 10,000: i (b) Complete the table, where the budget. B, is in dollars and the maximum production is the number of pairs of skis to be produced each week. Question 7 of 16 -/1 ini On B= 2000: i i i i On B = 4000:1 On B = 6000: i On B = 8000:( On B = 10,000: (b) Complete the table, where the budget. B. is in dollars and the maximum production is the number of pairs of skisto be produced each week. Round your answers to the nearest integer. B 2000 4000 6000 8000 10,000 M dM (c) Estimate the Lagrange multiplier 1 = at a budget of $2000. dB Round your answer to three decimal places