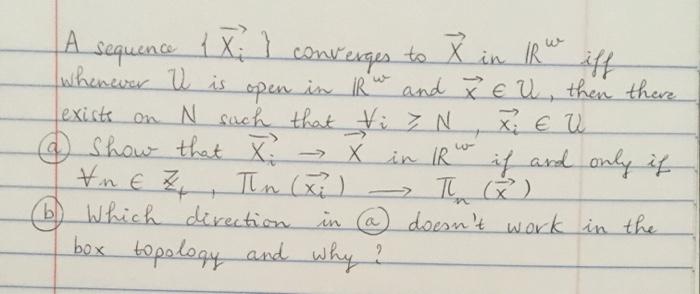
w sequence 1x } A converges Pin IR iff Whenever U is open in Rwand ze U, then there exists on N such that i 3 N. XE U @ Show that X X in IR' in IR if and only if Tin (xi) - The G (6) Which direction in @ doesn't work in the box topology and why ? tn E Z We know that , Tl An means Ti An * MEZ > IR w has the product topology It E Rw A typical basis element of Rw has this formi T (U) - (UM ... The (un) a finite intersection where for each itls. Anky U or is in IR & EZ+ Alternatively we could expren this some basis element of Rw this TL X; where {4, Kimli finite set of indices and if i 12, and then XR if and then Ui o R is , R open *xe B (x E B and B as a basis element B Bn A + 0 ) and Z E Th An Vn e Z. (Zn E An) z & T An In EZ (Z & An) B CR, then Z E T n (B) Zm E B and Z & T (B) ( Z & B ant a baris Z E T t (w) n t ( un... nt (U) Zie Ui for all 14, So to check membership of an element in a element, You need only check to see what's happening for finite number of indices. (The same indices where the basis element's X: + R) All projection functions are continuous so is the cu) in Rw U is + topen in R with only be a Let It be the subset of 1Rw that consists of all elesmentel a finite number of components nonzero fo. 11 consists of all those elements of that are eventually zewo. For example, L, L2, L3, ..., &n,0,0,0,0,0,... would typical element of IRO. Note that any element with an infinite number of nonzero components is not, in IR. For example 1,0, 1, 0, 1, 0, 1, ... 7 is not A converges to X in IR iff Whenever U is open in Rwand X c U, then there exists on N such that di N. XE U @ Show that X X X in IR if and only if In xil 6 Which direction in a doesn't work in the box topology and why ? in Roo sequence {x; } VnE Z w sequence 1x } A converges Pin IR iff Whenever U is open in Rwand ze U, then there exists on N such that i 3 N. XE U @ Show that X X in IR' in IR if and only if Tin (xi) - The G (6) Which direction in @ doesn't work in the box topology and why ? tn E Z We know that , Tl An means Ti An * MEZ > IR w has the product topology It E Rw A typical basis element of Rw has this formi T (U) - (UM ... The (un) a finite intersection where for each itls. Anky U or is in IR & EZ+ Alternatively we could expren this some basis element of Rw this TL X; where {4, Kimli finite set of indices and if i 12, and then XR if and then Ui o R is , R open *xe B (x E B and B as a basis element B Bn A + 0 ) and Z E Th An Vn e Z. (Zn E An) z & T An In EZ (Z & An) B CR, then Z E T n (B) Zm E B and Z & T (B) ( Z & B ant a baris Z E T t (w) n t ( un... nt (U) Zie Ui for all 14, So to check membership of an element in a element, You need only check to see what's happening for finite number of indices. (The same indices where the basis element's X: + R) All projection functions are continuous so is the cu) in Rw U is + topen in R with only be a Let It be the subset of 1Rw that consists of all elesmentel a finite number of components nonzero fo. 11 consists of all those elements of that are eventually zewo. For example, L, L2, L3, ..., &n,0,0,0,0,0,... would typical element of IRO. Note that any element with an infinite number of nonzero components is not, in IR. For example 1,0, 1, 0, 1, 0, 1, ... 7 is not A converges to X in IR iff Whenever U is open in Rwand X c U, then there exists on N such that di N. XE U @ Show that X X X in IR if and only if In xil 6 Which direction in a doesn't work in the box topology and why ? in Roo sequence {x; } VnE Z