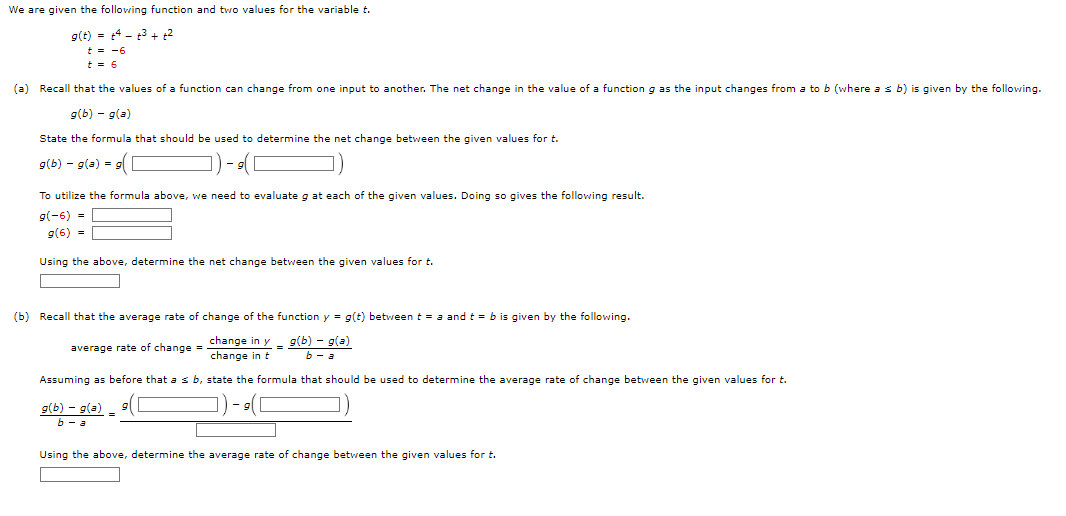
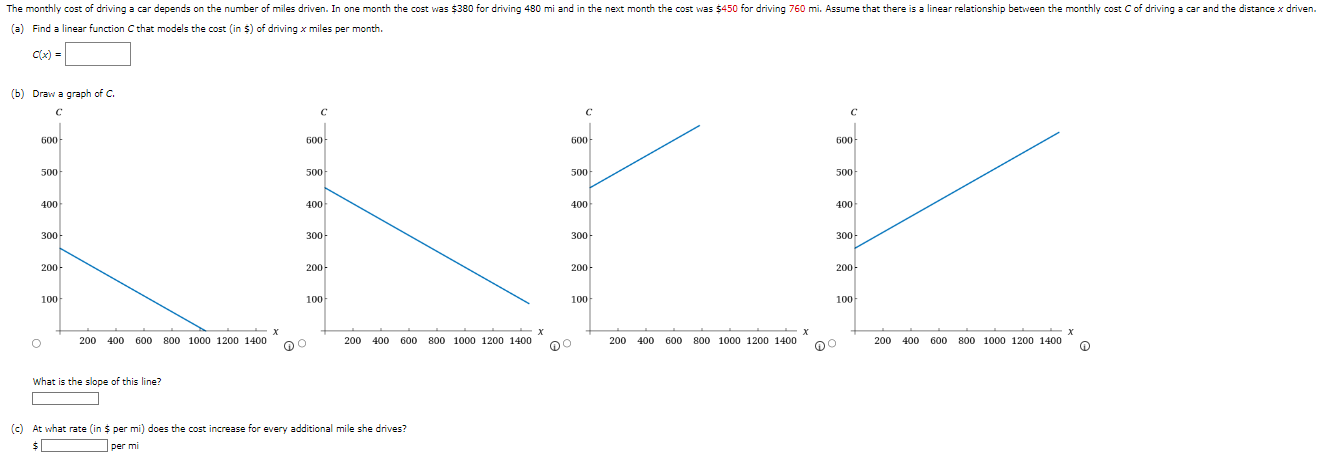
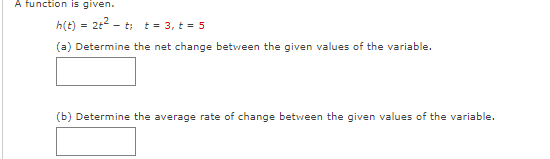
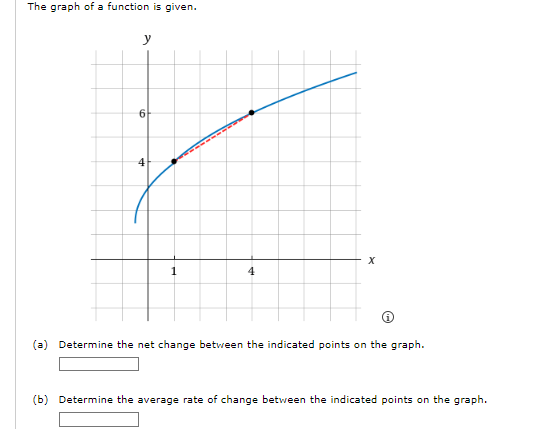
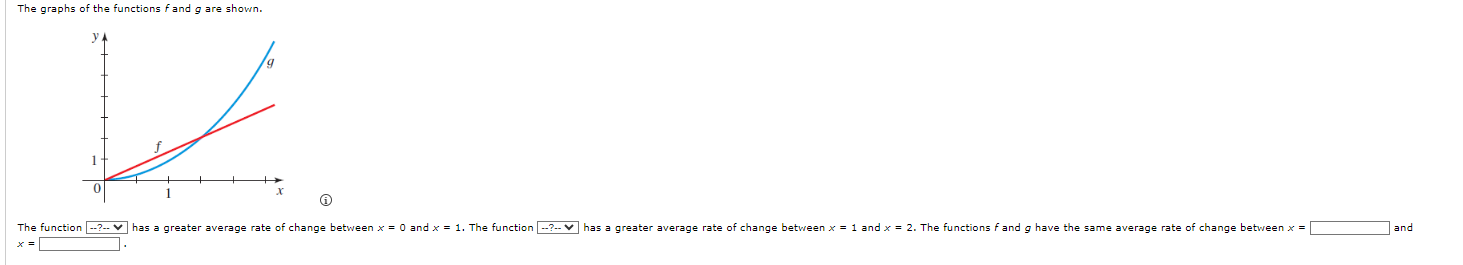
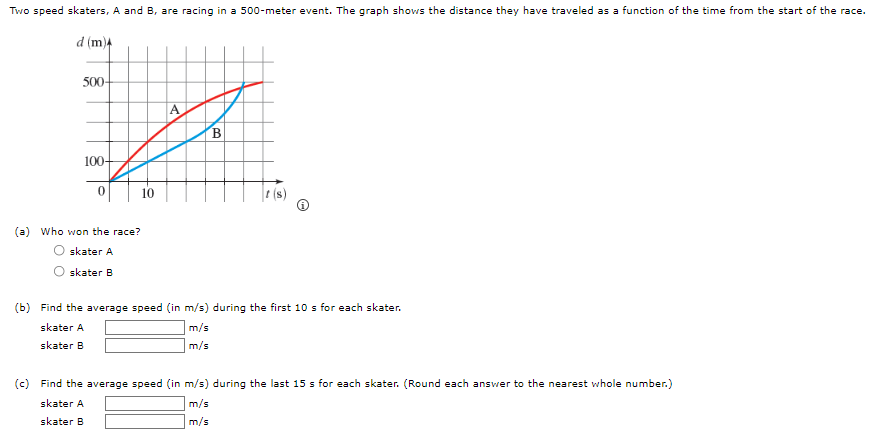
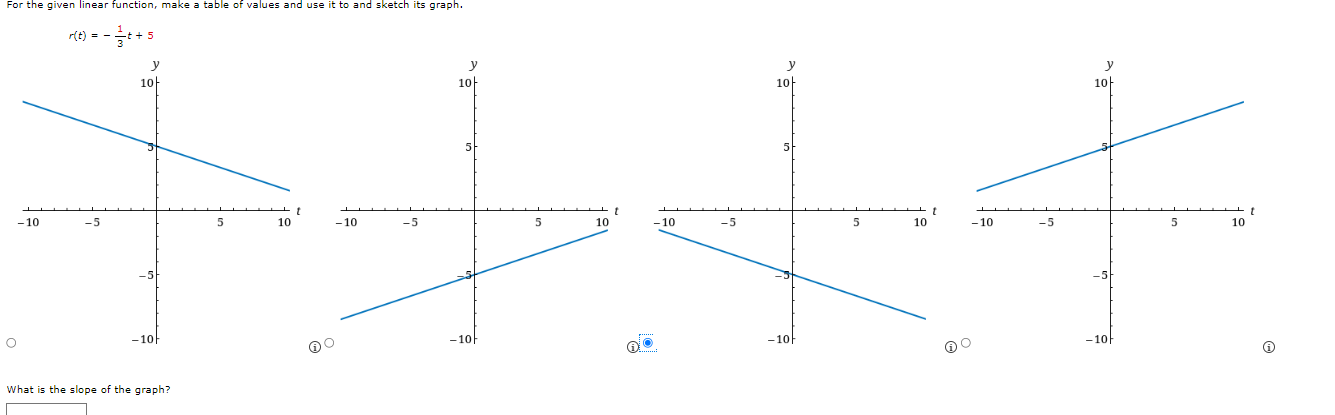
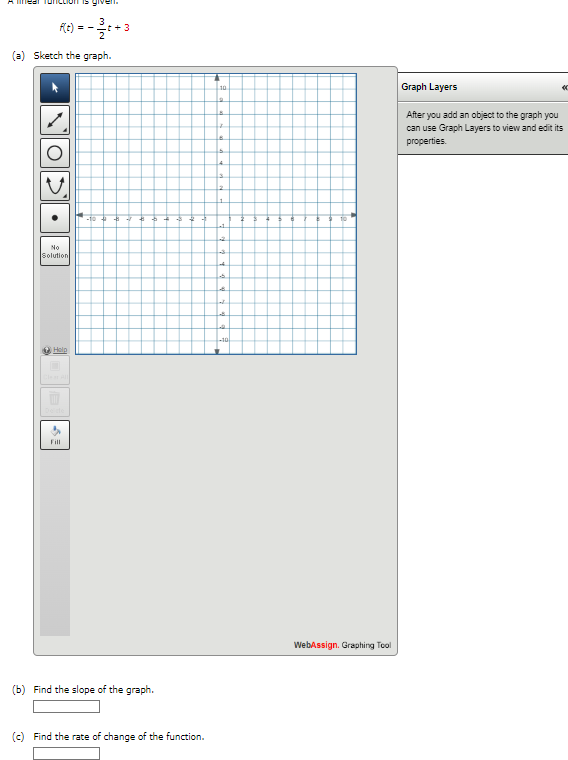
We are given the following function and two values for the variable t. g (t) = 4 - 13+ +2 t= -6 + = 6 (a) Recall that the values of a function can change from one input to another, The net change in the value of a function g as the input changes from a to b (where a s b) is given by the following. g(b) - g(=) State the formula that should be used to determine the net change between the given values for t. g(b) - g(=) = \\\\ To utilize the formula above, we need to evaluate g at each of the given values. Doing so gives the following result. 9(-6) = g(6) = Using the above, determine the net change between the given values for t. (b) Recall that the average rate of change of the function y = g(t) between t = = and t = b is given by the following. average rate of change _ change in y _ g(b) - g(=) change in t b - a Assuming as before that a s b, state the formula that should be used to determine the average rate of change between the given values for t. g(b) - g(=) b - a Using the above, determine the average rate of change between the given values for t.The monthly cost of driving a car depends on the number of miles driven. In one month the cost was $380 for driving 480 mi and in the next month the cost was $450 for driving 760 mi. Assume that there is a linear relationship between the monthly cost C of driving a car and the distance x driven. (=) Find a linear function C that models the cost (in $) of driving x miles per month. (x) = (b) Draw a graph of C. 600 600- 600 600 500 500 500 500 400 400 400 400 300 300 300 300 200 200 200 200- 100 100 100 100 X 200 400 600 800 1000 1200 1400 200 400 600 800 1000 1200 1400 200 400 600 800 1000 1200 1400 - X 200 400 600 800 1000 1200 1400 What is the slope of this line? (c) At what rate (in $ per mi) does the cost increase for every additional mile she drives? $ per miA function is given. h(t) = 2+