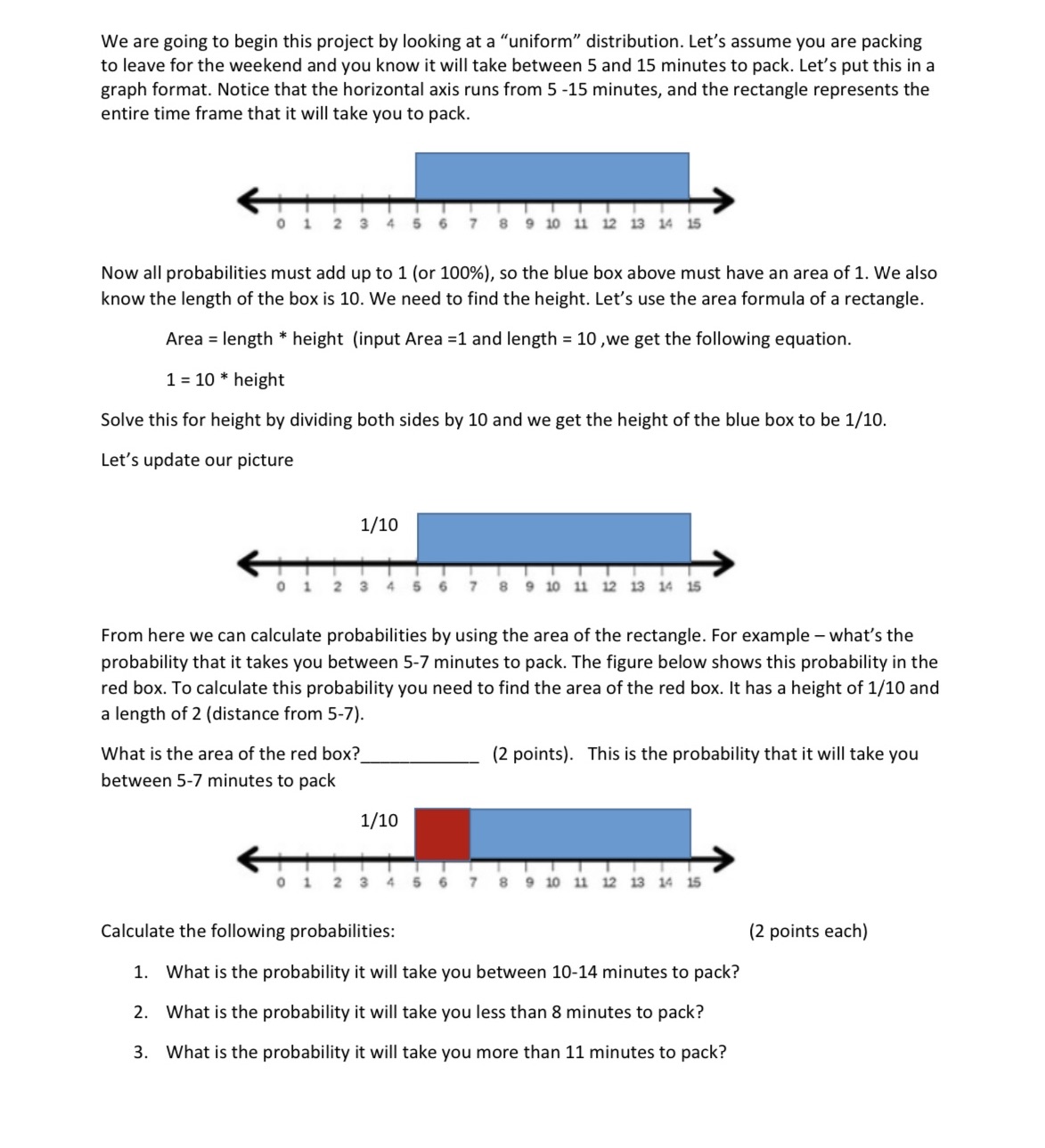
We are going to begin this project by looking at a \"uniform" distribution. Let's assume you are packing to leave for the weekend and you know it will take between 5 and 15 minutes to pack. Let's put this in a graph format. Notice that the horizontal axis runs from 5 -15 minutes, and the rectangle represents the entire time frame that it will take you to pack. Ol23456?8910u12131'-L5 Now all probabilities must add up to 1 (or 100%), so the blue box above must have an area of 1. We also know the length of the box is 10. We need to find the height. Let's use the area formula of a rectangle. Area = length * height (input Area =1 and length = 10 ,we get the following equation. 1 = 10 * height Solve this for height by dividing both sides by 10 and we get the height of the blue box to be 1/10. Let's update our picture 012311567891011L2L3ML5 From here we can calculate probabilities by using the area of the rectangle. For example what's the probability that it takes you between 5-7 minutes to pack. The figure below shows this probability in the red box. To calculate this probability you need to find the area of the red box. It has a height of 1/10 and a length of 2 (distance from 5-7}. What is the area of the red box? (2 points). This is the probability that it will take you between 5-7 minutes to pack 1/10 0123456789101112131415 Calculate the following probabilities: (2 points each) 1. What is the probability it will take you between 10-14 minutes to pack? 2. What is the probability it will take you less than 8 minutes to pack? 3. What is the probability it will take you more than 11 minutes to pack