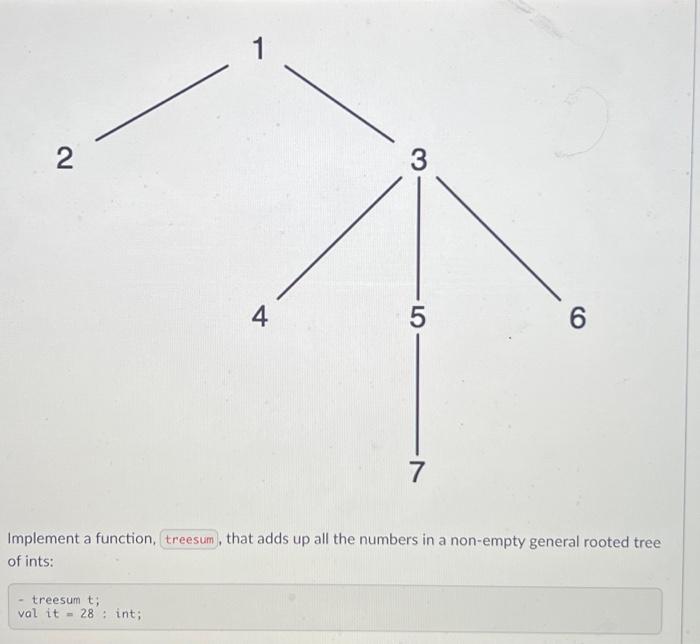
We can define a general rooted tree to be a tree that has any number of subtrees hanging from each node, not just two. To implement such a tree, we can just define a list of subtrees in each node: datatype 'a tree= Node of 'a 'a tree list; (A pair: Note no 'I' *) We won't need Empty here because we can just use nil) in the second slot for leaves of the tree, and to keep things simple for this problem we're not going to worry about having an altogether empty tree. You only have to process Nodes. A sample definition of a tree would be: Node(1, [Node(2, nil), Node(3, [Node(4, nil), Node(5, [Node(7,nil)]), Node (6,nil)])]) val t- which looks like the following: 2 - 1 treesum t; val it 28: int; 4 3 5 7 6 Implement a function, treesum, that adds up all the numbers in a non-empty general rooted tree of ints: