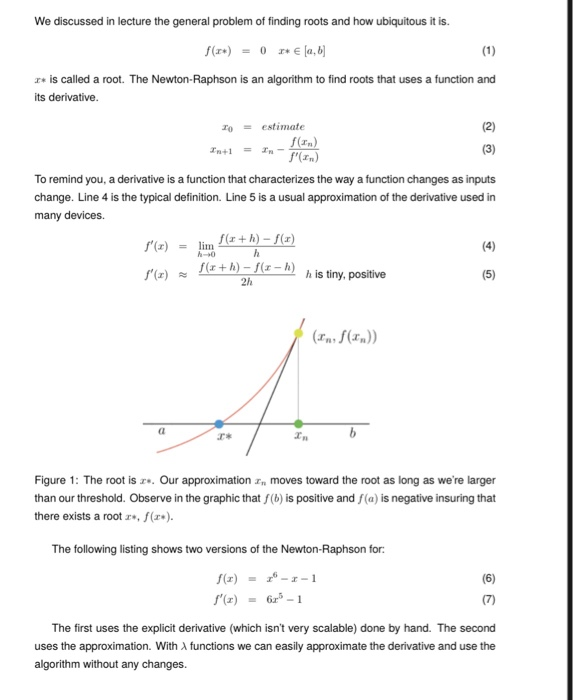
We discussed in lecture the general problem of finding roots and how ubiquitous it is. r is called a root. The Newton-Raphson is an algorithm to find roots that uses a function and its derivative 10 estimate fan To remind you, a derivative is a function that characterizes the way a function changes as inputs change. Line 4 is the typical definition. Line 5 is a usual approximation of the derivative used in many devices. f(r + h) -f(r) r +h) - f(r-h) h is tiny, positive 2h r* Figure 1: The root is . Our approximation n moves toward the root as long as we're larger than our threshold. Observe in the graphic that f(b) is positive and f(a) is negative insuring that there exists a root , f(r.). The following listing shows two versions of the Newton-Raphson for f(x)--1 r(z) -62s-1 The first uses the explicit derivative (which isn't very scalable) done by hand. The second uses the approximation. With functions we can easily approximate the derivative and use the algorithm without any changes