We have a curve in space given by an unspecified parameter representation r(t) for t≥0. We can think of theparameter representation as the description of the path of a particle moving in space.
At a given time t=a, the speed is

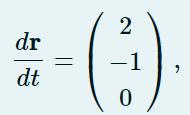
the acceleration is

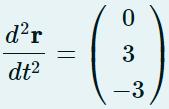
and the derivative of the acceleration ( the pressure) is

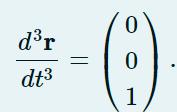
Use the velocity vector to calculate the unit tangent vector T^ when t=a and enter the components of the vector below. The answers must be in symbolic form.

x-coordinate:

y coordinate:

z coordinate:

b)

Calculate the vector B^ and unit normal vector N^=B^×T^ when t=a and enter the components of N^ below. The answers must be in symbolic form.

x-coordinate:

y coordinate:

z coordinate:

c)

Also calculate curvature and torsion and enter the answers below in symbolic form.

κ=

τ=

Transcribed Image Text:

dr dt = 2 -1 0 dr dt = 2 -1 0

Answer rating: 100% (QA)

a To calculate the unit tangent vector T we can normalize the velocity vector The velocity vector is ... View the full answer