We learned that a binomial tree of order i can be formed by taking two copies of a binomial tree of order i 1 and letting the root of one tree have the other tree as its first child. Consider the following definition of Fibomial trees: A Fibomial tree of order 0 is a single node and a Fibomial tree of order 1 is also a single node. A Fibomial tree of order i is formed by taking a Fibomial tree of order i 1 and a Fibomial tree of order i 2 letting the root of the first tree (of order i 1) have the other tree as its first child (see the figure below).

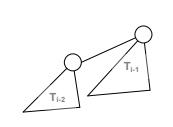
Figure 1: Forming a Fibomial tree of order i from two Fibomial trees of orders i 1 and i 2.

a) Draw a Fibomial tree of order i = 5.

b) Indicate whether the following statement is correct or not. Provide a justification of your answer.

Let Tk denote the Fibomial tree of order k. The children of the root of Tk are the Fibomial trees Tk2, Tk3, . . . , T2, T1, T0, T0 (more precisely, there is exactly one copy of each Ti for i {k 2, k 3, . . . , 1} and two copies of T0 as a children of Tk). c) Indicate how many nodes exist in a Fibomial tree of order k. You should provide a recursive formula and relate it to a known series.

d) Indicate what the height of a Fibomial tree of order k is. Again, you should provide a recursive formula and solve it.

TH1 Ti-2