Question: We want to compute an approximation to e1/6 given by Pn(1/6) where Pn(x) is the Taylor polynomial of degree n about a=0 of the function

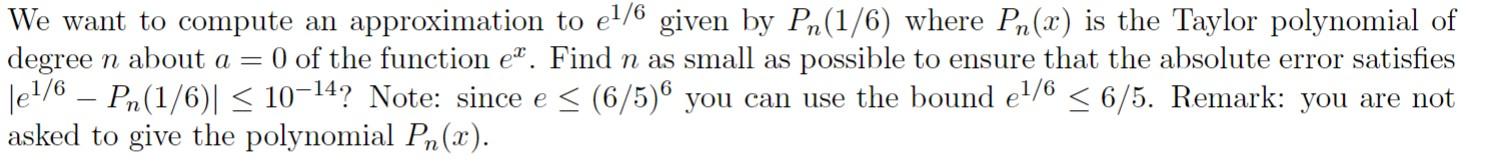
We want to compute an approximation to e1/6 given by Pn(1/6)

We want to compute an approximation to e1/6 given by Pn(1/6) where Pn(x) is the Taylor polynomial of degree n about a=0 of the function ex. Find n as small as possible to ensure that the absolute error satisfies e1/6Pn(1/6)1014 ? Note: since e(6/5)6 you can use the bound e1/66/5. Remark: you are not asked to give the polynomial Pn(x)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

We want to compute an approximation to e/6 given by Pn(1/6) where Pn(x) is the Taylor polynomial of degree n about a = 0 of the function e. Find n as small as possible to ensure that the absolute...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Describe how to construct the function cpo ((D E), v) of two cpos (D, vD) and (E, vE). Prove that ((D E), v) is a cpo. (You may use facts about least upper bounds provided you state them clearly.)...

1. (1 point) Find all numbers c that satisfy the conclusion of Rolle's The- orem for the following function and interval. Enter the values in increasing order and enter N in any blanks you don't need...

To practice basic Python programming of control and data structures. Spend time testing and debugging your work. Get experience looking up background material on the Internet. For the 1st item, you...

In this problem, you will use a linear approximation to approximate V493. Let an) = E The linear approximation of f(C) at w = 49 can be written in the form L(:L') = ma: + b' Compute m and b. c l |...

Downloaded 02/28/15 to 132.174.255.3. Redistribution subject to SIAM license or copyright; see http://www.siam.org/journals/ojsa.php 15.7. Exercises 475 changes and we laugh no more. While...

dterm Examination CSCI 3231 Spring, 2005 ___________ Your Name .. Please answer each question by entering the most nearly correct answer (a, b, c, d) in the blank on the left. ___/_1. The...

Every time I run this code I get this error message The Taylor polynomial is a powerful tool for approximation The Taylor polynomial of degree n for ex, for any given x, is r" n! ending in x White a...

Boot time (the time between the appearance of the Bios screen to the first file that is loaded in Windows) on Eric Mousers personal computer follows an exponential distribution with a mean of 27...

A fishing company would like to predict how much fish are caught based on the amount of baits used. You are brought in as a consultant. You believe a linear regression model may be appropriate. Using...

What is the value of their stock when the required rate of return is 1 4 1 3 percent? Multiple Choice $ 3 . 9 2 $ 4 3 . 3 6 $ 4 9 . 0 0

The artisan wines is a retail store selling vintage wines on December 31, 2019 the firms general ledger contain the accounts in balance is below all account balances are normal The Artisan Wines is a...