We will write pseudocode to solve a Sudoku based on a backtracking approach. A Sudoku is a 9 by 9 puzzle where puzzler attempts to fill in each cell with numbers from 1 to 9 satisfying three criteria:

• Each row has the number from 1 to 9 exactly once.
• Each column has the numbers from 1 to 9 exactly once.
• Each of the 9 three by three sub-grids has the numbers from 1 to 9 exactly once.

The following is an example puzzle on the left with the 9 sub-grids bolded and the accompanying solutions on the right.

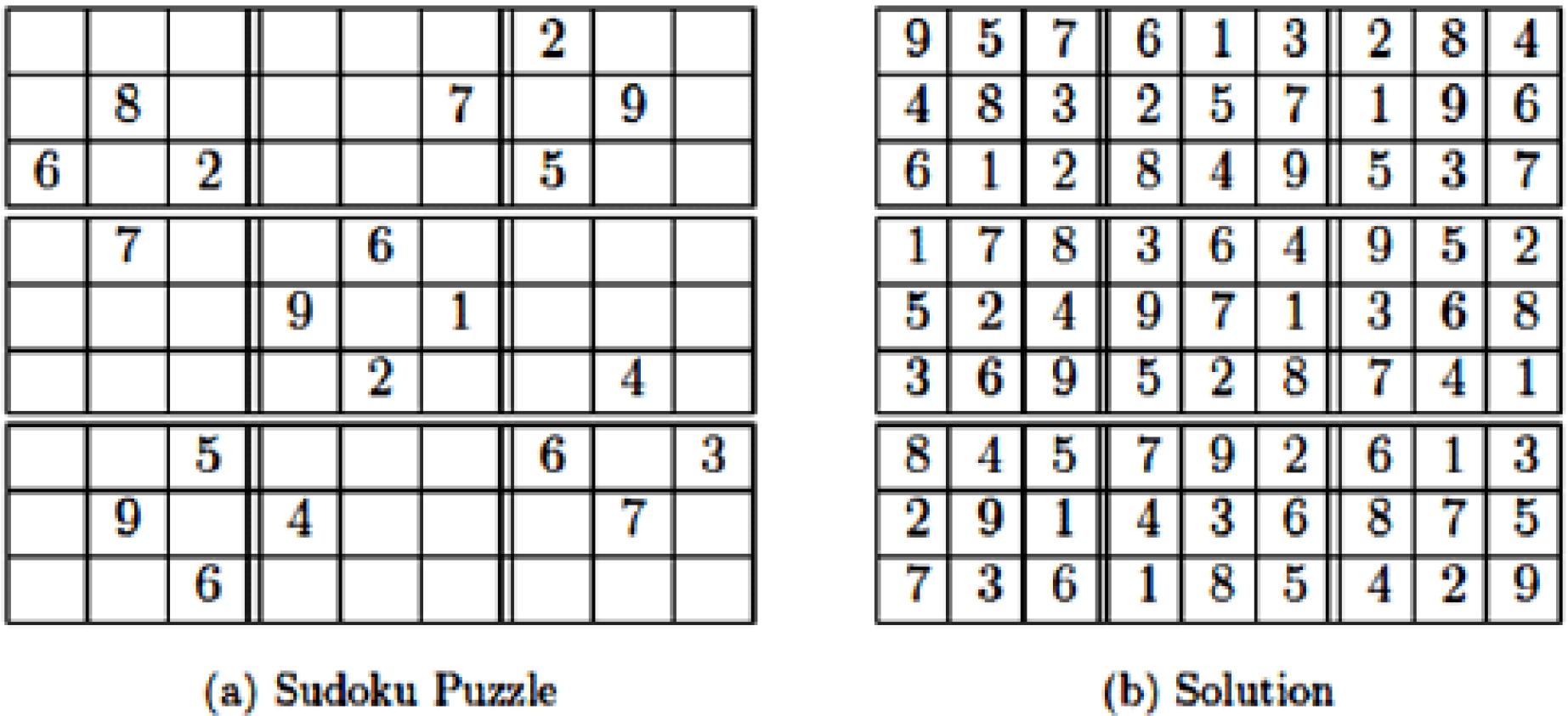
For this we will introduce a new SUDOKU data type with the following operations

• MAKEEMPTYSUDOKU • ITEM(S, row, col)

• FILL(S, row, col, number) • SUBGRID(S, row, col)

• BLANK(S, row, col) • ROW(S, row)

• ISBLANK(S, row, col) • COL(S, col)

Above, ROW and COL return a list consisting of the numbers in the given row/column. SUBGRID returns a list of the numbers in the same sub-grid as the cell in row, col. The sub-grid is one of the nine sub-grids found above. For example, SUBGRID(S, 5, 5) would return the 9 numbers in the middle most sub-grid as a list. FILL returns a new SUDOKU grid with the number _lled in position (row, col).

Modify the backtracking algorithm from the course to write a Sudoku solver, that is, write an algorithm that solves the following problem:

SOLVE SUDOKU(S)

INPUT: A partially filled Sudoku S that obeys the above constraints.

OUTPUT: A filled Sudoku S satisfying the above constraints or False if impossible.

You do not need to be too formal with your pseudocode approach but should be able to describe your algorithm to a competent reader.
 

00 8 7 2 9 CO 6 2 107 5 95761 13 28 4 483 946 25 57 12 284 49 196 53 7 7 6 1 78 36 64 95 9 1 52 24 9 71 368 2 4 3 69 5 28 741 5 6 3 8 45 79 92 61 9 7 29 91 43 36 87 -28-35 6 73 36 1 85 42 9 Sudoku Puzzle (b) Solution