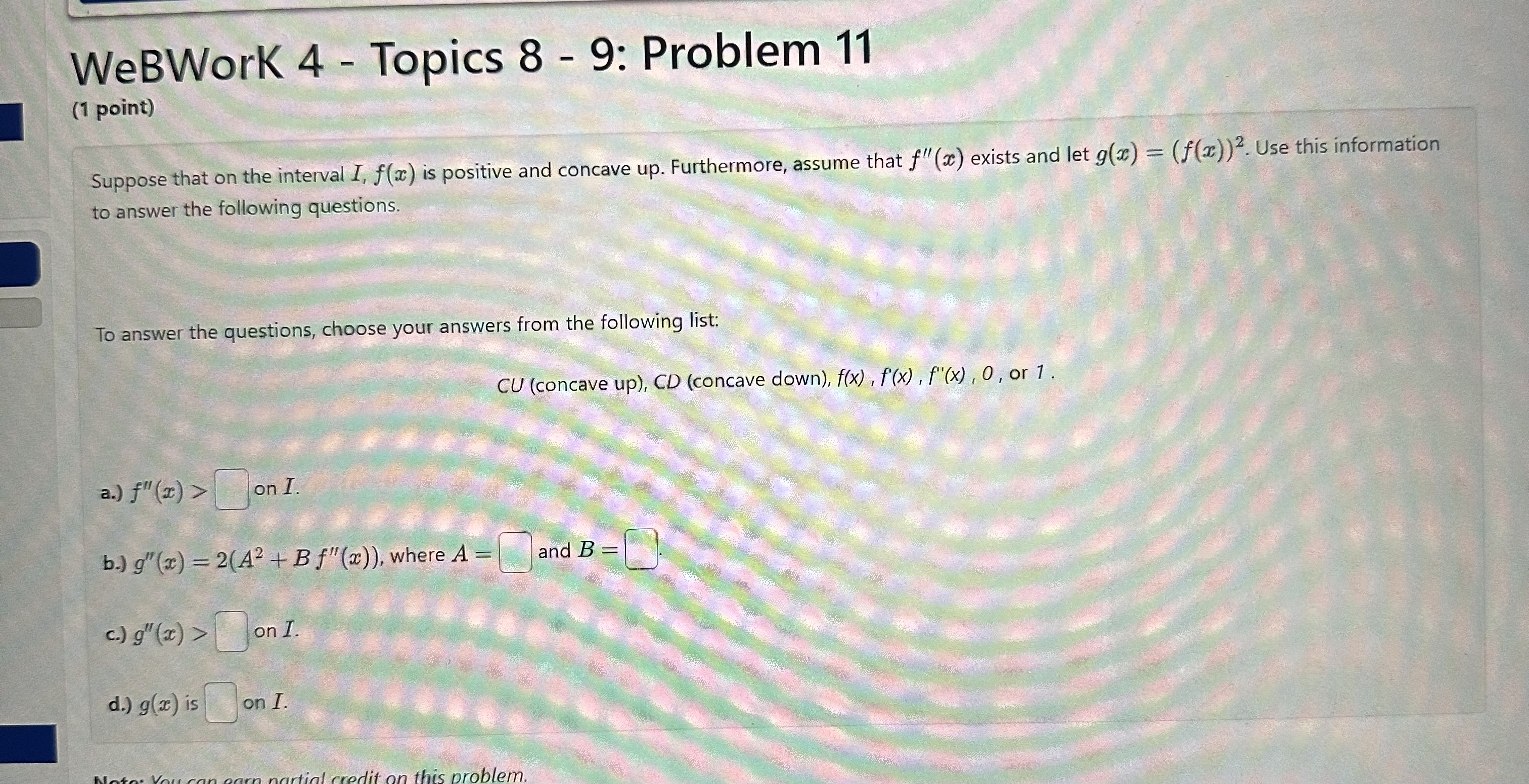
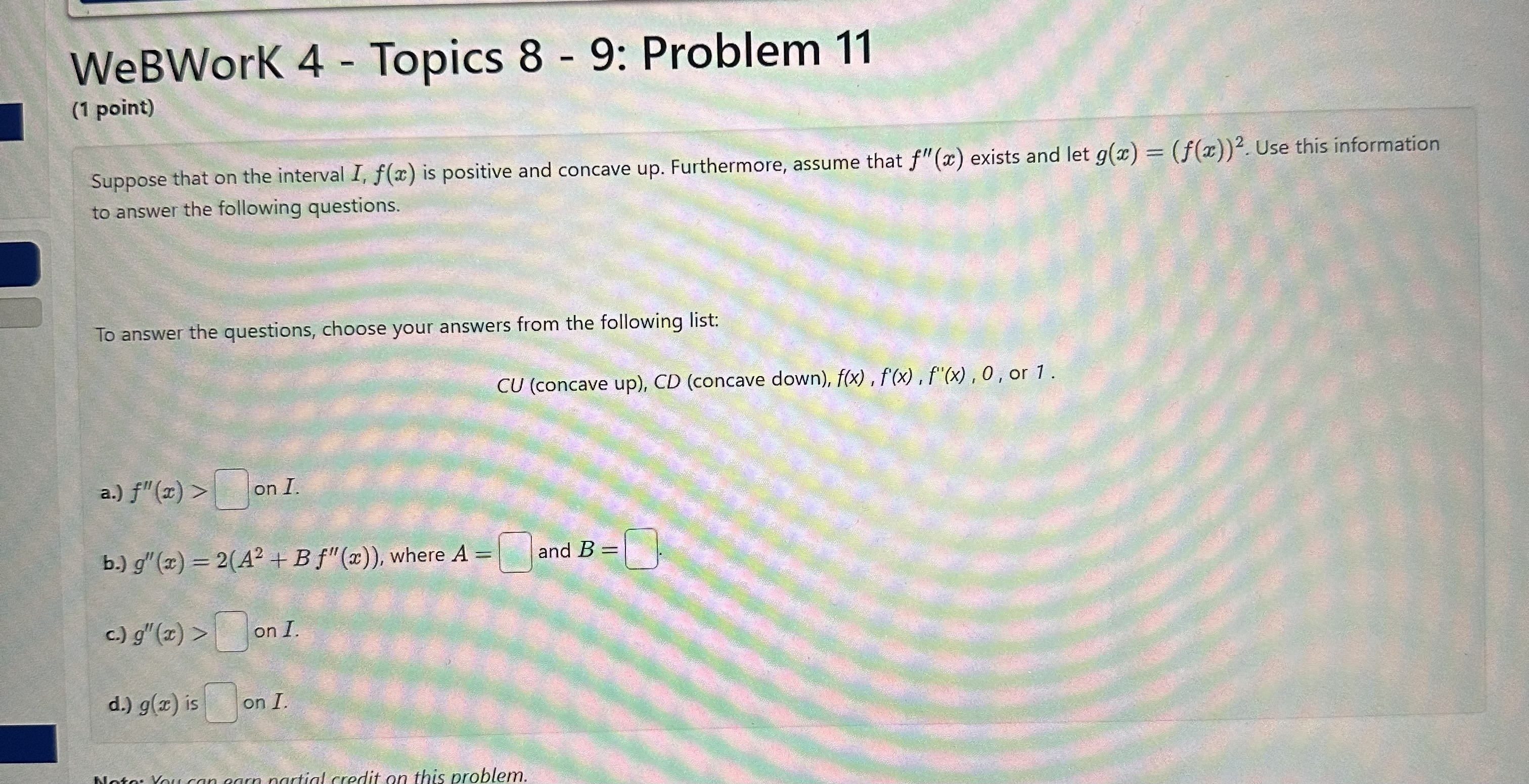
WeBWork 4 - Topics 8 - 9: Problem 7 (1 point) A cylindrical can, open at the top, is to hold 280 cm3 of liquid. Find the height and radius that minimize the amount of material needed to manufacture the can. Enter your answer with rational exponents, and use pi to represent . Radius= Height= redit on this problem.WeBWork 4 - Topics 8 - 9: Problem 8 (1 point) A rectangular storage container with an open top is to have a volume of 64m'. The length of its base is twice the width. Material for the base costs $18 per square meter. Material for the sides costs $24 per square meter. Find the dimensions and the cost of materials for the cheapest such container. . Width: m . Length: m . Height: m . Cost: $WeBWork 4 - Topics 8 - 9: Problem 10 (1 point) Consider the function f(x) = -2x3+ 24x2 -72x + 2. For this function there are three important intervals: (-co, A], [A, B], and [B, co) where A and B are the critical points Find A and B For each of the following intervals, tell whether f(x ) is increasing (type in INC) or decreasing (type in DEC). (-00, A]: [A, B]: [B, 00): Note: You can earn partial credit on this problem.WeBWork 4 - Topics 8 - 9: Problem 11 (1 point) Suppose that on the interval I, f(x) is positive and concave up. Furthermore, assume that f"(x) exists and let g(x) = (f(x))2. Use this information to answer the following questions. To answer the questions, choose your answers from the following list: CU (concave up), CD (concave down), f(x) , f'(x) , f"(x) , 0, or 1. a.) f" (a) > on I. b.) g" (x) - 2(A2 + B f"(2)), where A = and B = c.) g" (3) > on I. d.) g(x) is on I this