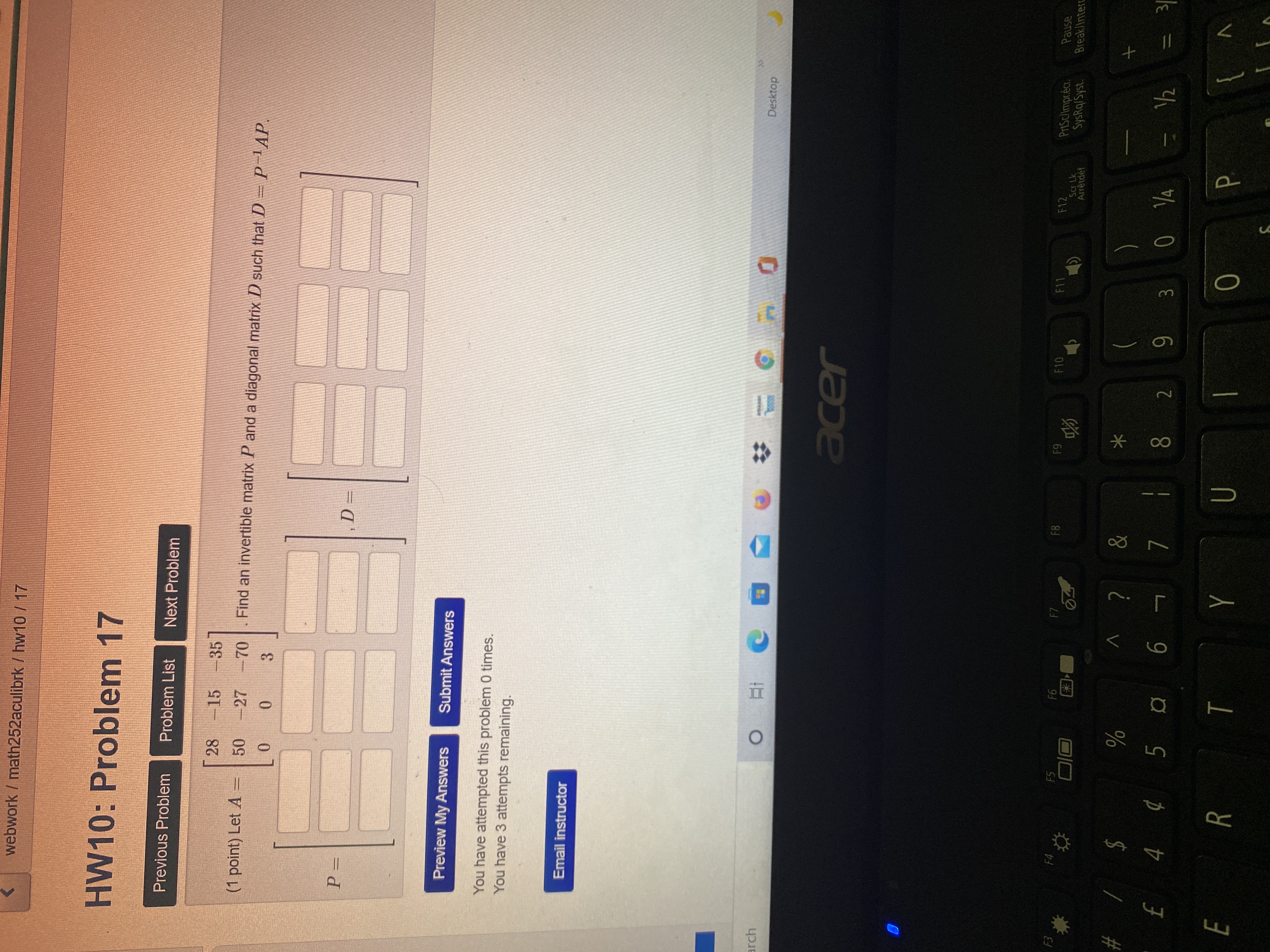
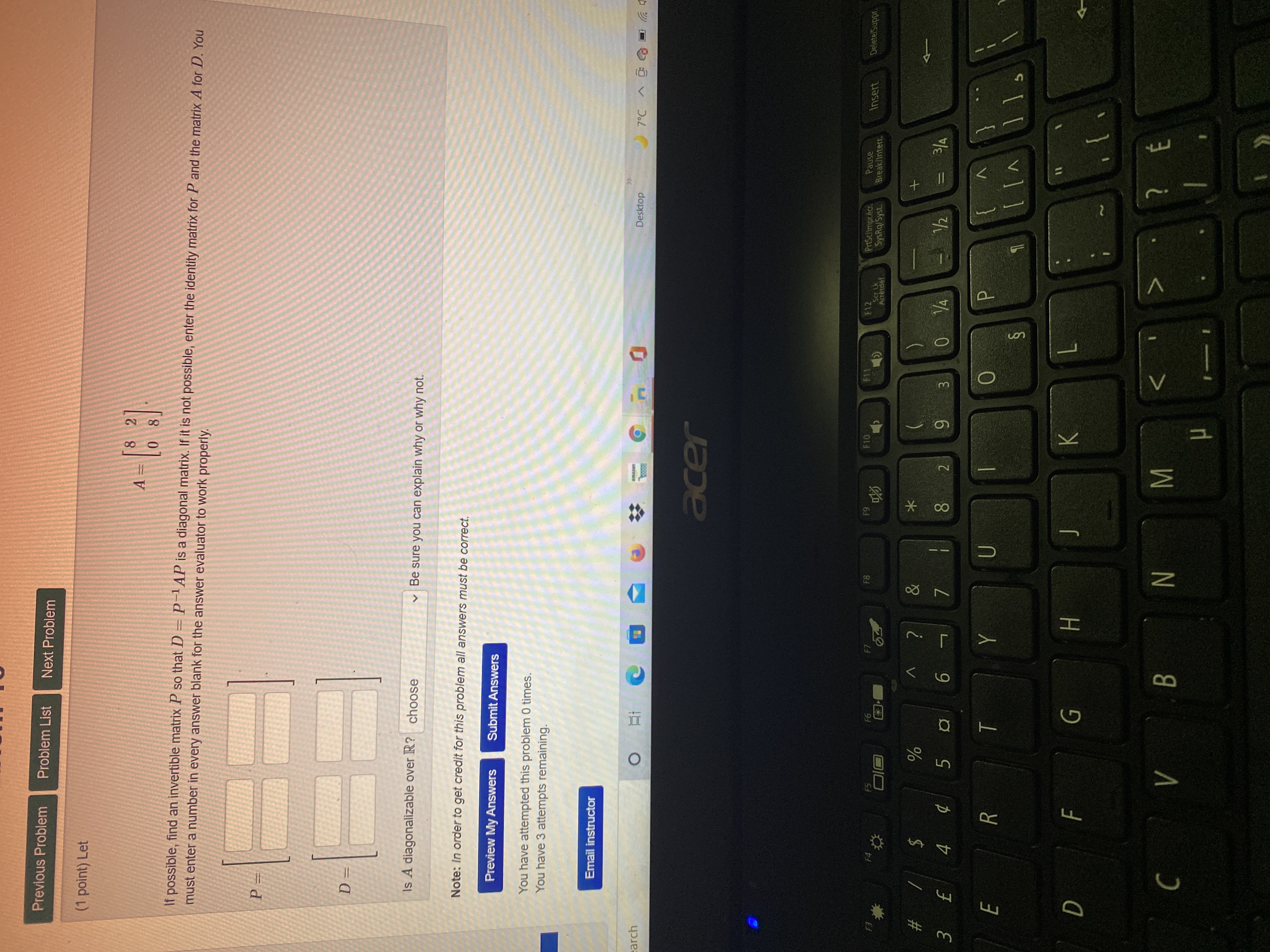
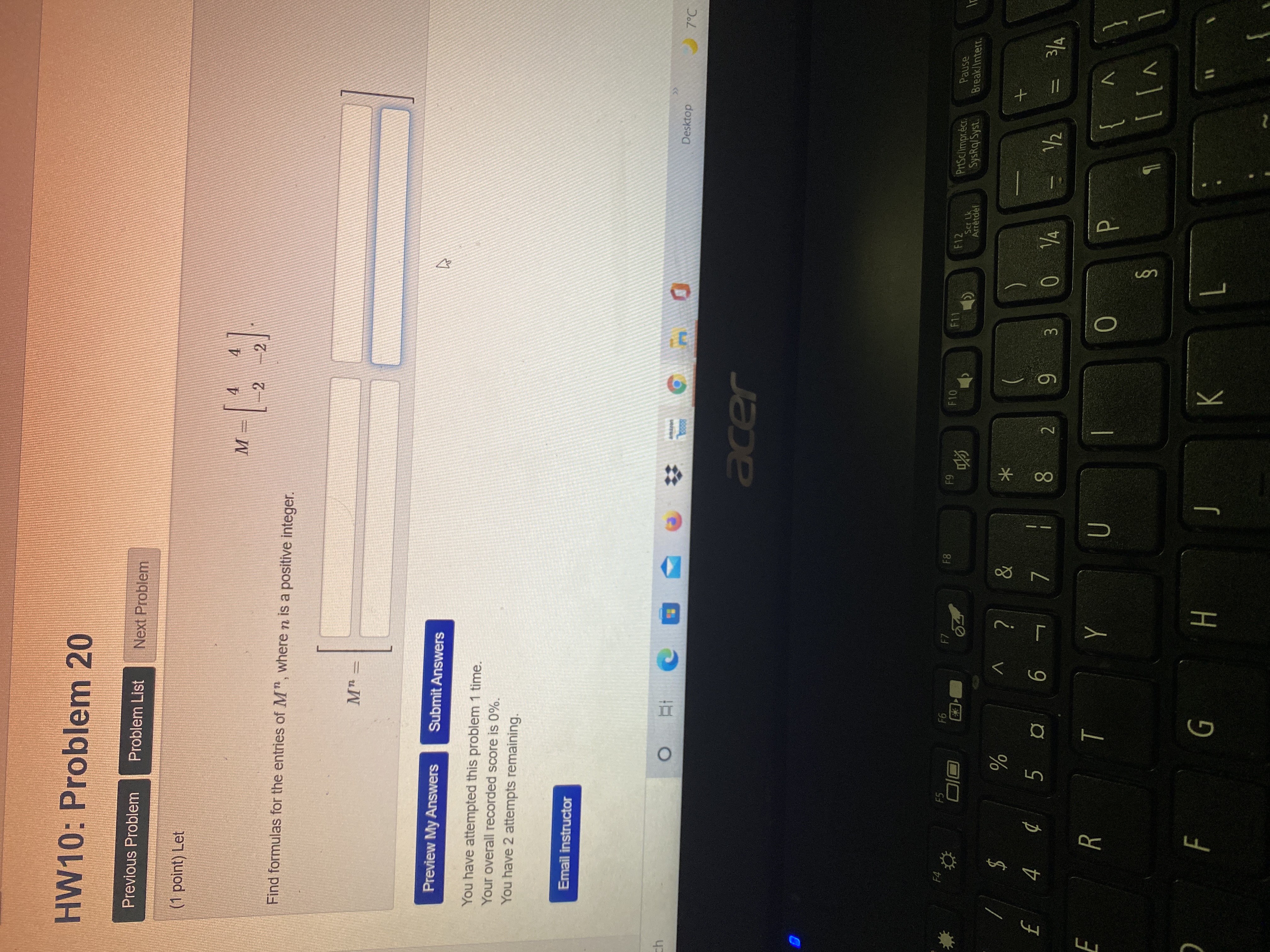
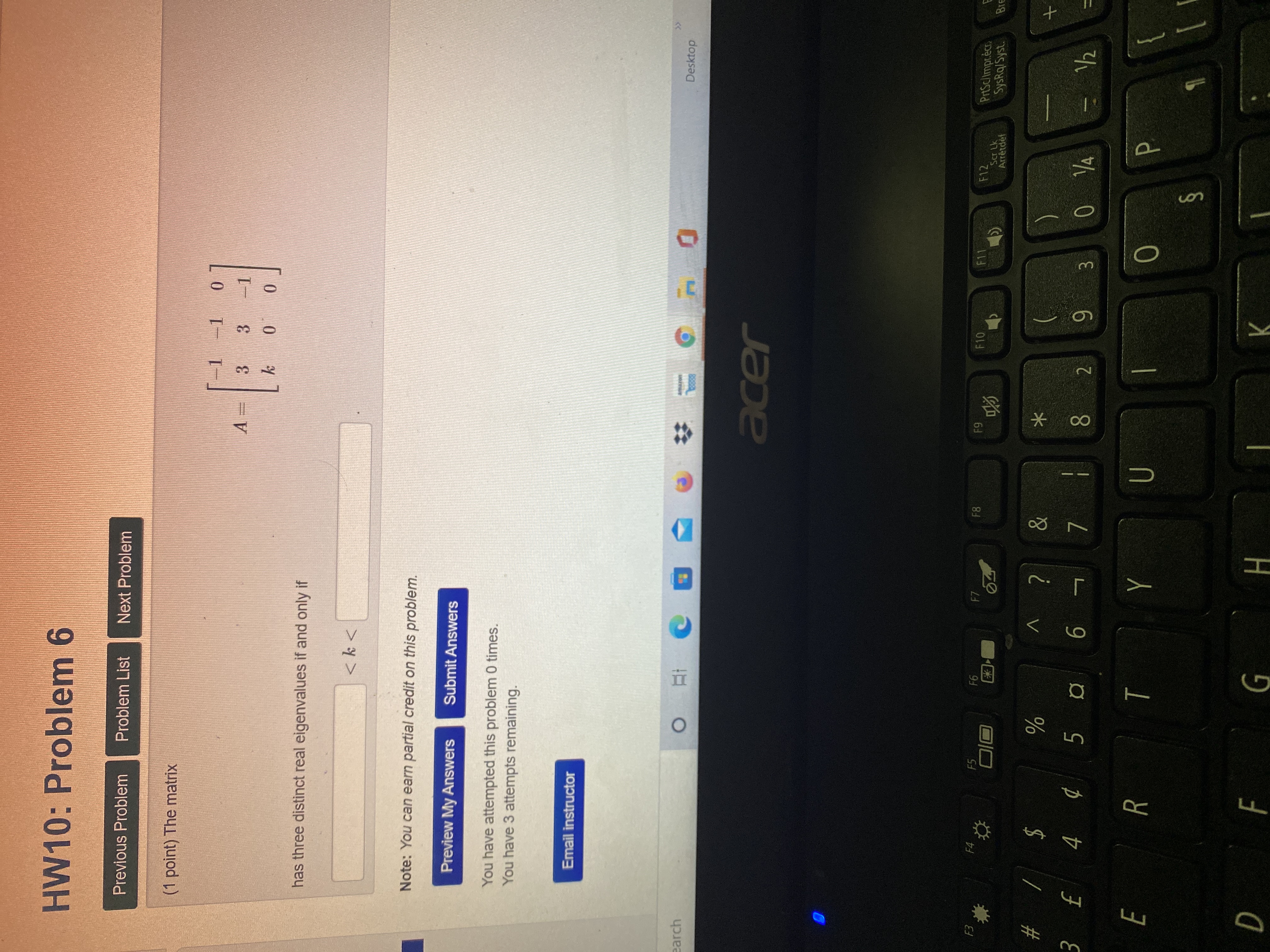
Question: webwork / math252aculibrk / hw10 / 17 HW10: Problem 17 Previous Problem Problem List Next Problem 28 -15 -35 (1 point) Let A = 50
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


