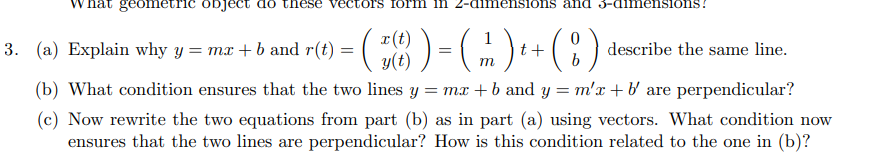
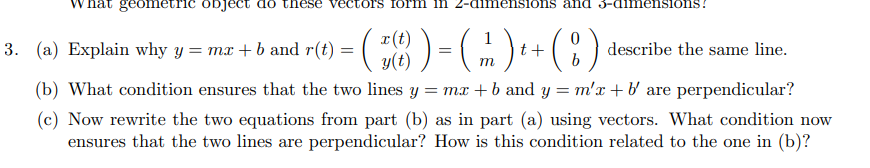
what geometric object do these vectors form In Z-dimensions and 5-dimensions ! 3. (a) Explain why y = mr + b and r(t) = ( #8 ) = (m ) t+ (" ) describe the same line, (b) What condition ensures that the two lines y = mr + b and y = m'x + b' are perpendicular? (c) Now rewrite the two equations from part (b) as in part (a) using vectors. What condition now ensures that the two lines are perpendicular? How is this condition related to the one in (b)?5. The dot product you have encountered in the reading is explicitly defined for 2 and 3 dimensions. (a) Define a dot product for two vectors in any dimension k similar to the ones you have seen. (b) Use your dot product to calculate the angle between the vectors (-V3, 0, -1,0) and (1, 1, 0, 1). (c) Find a vector that is orthogonal to (-V3, 0, -1, 0) with regards to your dot product