What is the time complexity of the baseball elimination algorithm?

"In the baseball elimination problem there are n teams competing in a league. At a specific stage of the league season, w_i is the number of wins and r_i is the number of games left to play for team i and r_ij is the number of games left against team j. A team is eliminated if it has no chance to finish the season in the first place. The task of the baseball elimination problem is to determine which teams are eliminated at each point during the season. Schwartz^[13] proposed a method which reduces this problem to maximum network flow. In this method a network is created to determine whether team k is eliminated.

Let G = (V, E) be a network with s,t V being the source and the sink respectively. One adds a game node {i,j} with i j to V, and connects each of them from s by an edge with capacity r_ij which represents the number of plays between these two teams. We also add a team node for each team and connect each game node {i,j} with two team nodes i and j to ensure one of them wins. One does not need to restrict the flow value on these edges. Finally, edges are made from team node i to the sink node t and the capacity of w_k+r_kw_i is set to prevent team i from winning more than w_k+r_k. Let S be the set of all teams participating in the league and let {\displaystyle \scriptstyle r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\},i. In this method it is claimed team k is not eliminated if and only if a flow value of size r(S {k}) exists in network G. In the mentioned article it is proved that this flow value is the maximum flow value from s to t."

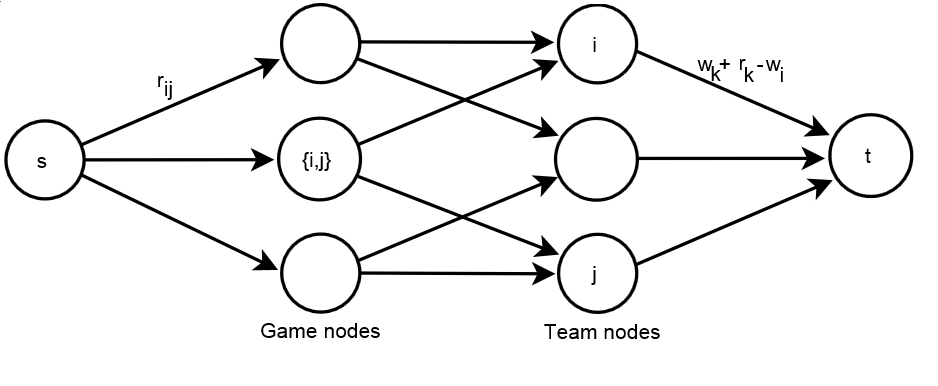
Need help finding the time complexity for the above algorithm..