When we estimate distances from velocity data, it is sometimes necessary to use times

t$0,$

t$1,$

t$2,$

t$3,$

that are not equally spaced. We can still estimate distances using the time periods

$$ti $=$ ti $$ ti$1.$

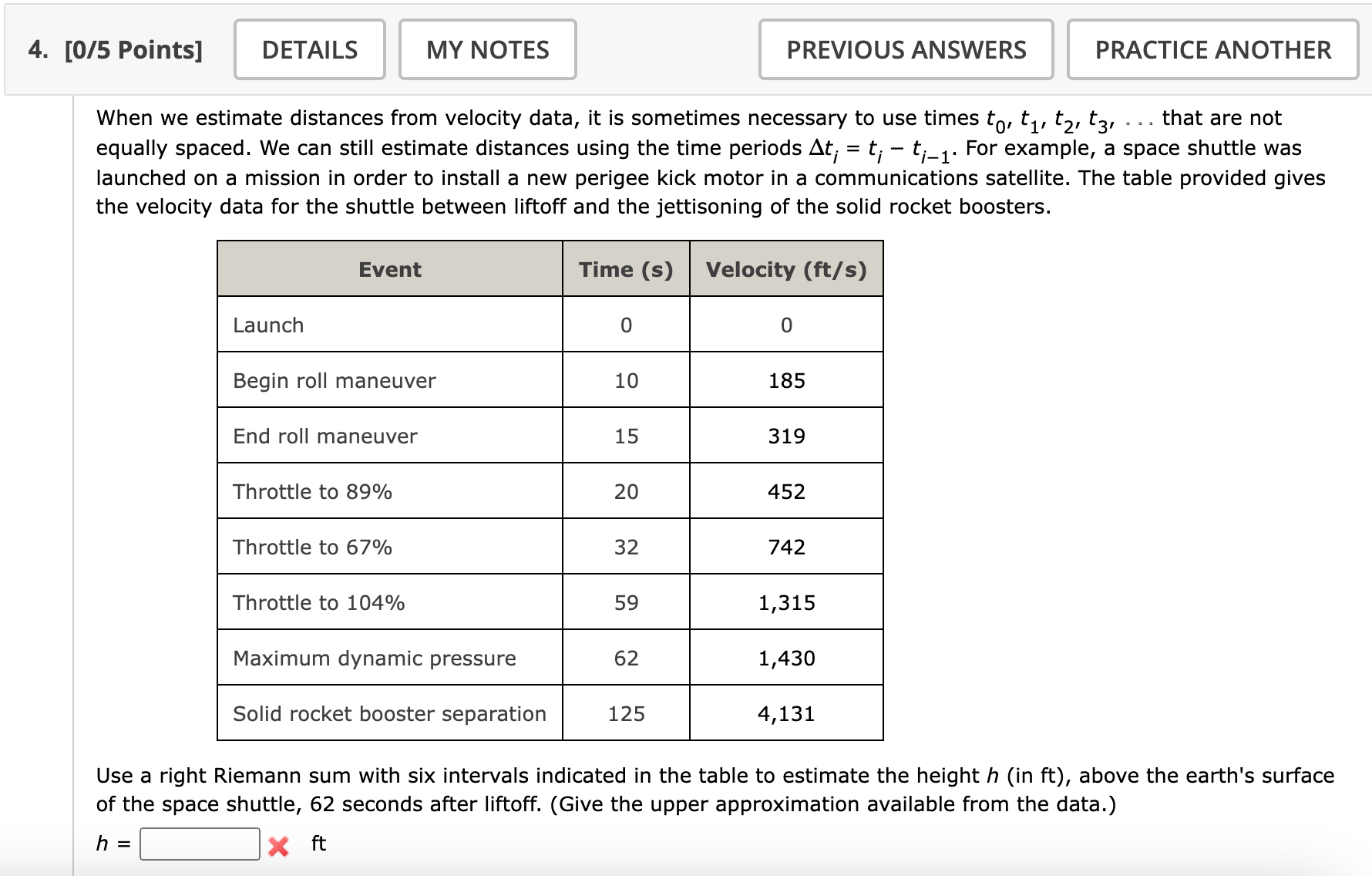
For example, a space shuttle was launched on a mission in order to install a new perigee kick motor in a communications satellite. The table provided gives the velocity data for the shuttle between liftoff and the jettisoning of the solid rocket boosters.

EventTime $($s$)$Velocity $($ft$/$s$)$Launch$00$Begin roll maneuver$10185$End roll maneuver$15319$Throttle to $89\%20452$Throttle to $67\%32742$Throttle to $104\%591,315$Maximum dynamic pressure$621,430$Solid rocket booster separation$1254,131$

Use a right Riemann sum with six intervals indicated in the table to estimate the height h $($in ft$),$ above the earth's surface of the space shuttle, $62$ seconds after liftoff. $($Give the upper approximation available from the data.$)$

h $=$ ft $4.[0/5$ Points$]$

When we estimate distances from velocity data, it is sometimes necessary to use times $\backslash ($ t$\_\{0\},$ t$\_\{1\},$ t$\_\{2\},$ t$\_\{3\},\backslash$ldots $\backslash )$ that are not equally spaced. We can still estimate distances using the time periods $\backslash (\backslash$Delta t$\_\{$i$\}=$t$\_\{$i$\}-$t$\_\{$i$-1\}\backslash ).$ For example, a space shuttle was launched on a mission in order to install a new perigee kick motor in a communications satellite. The table provided gives the velocity data for the shuttle between liftoff and the jettisoning of the solid rocket boosters.

$\backslash$begin$\{$tabular$\}\{|$l$|$c$|$c$|\}$

$\backslash$hline $\backslash$multicolumn$\{1\}\{|$c$|\}\{$ Event $\}$ & Time $($s$)$ & Velocity $($ft$/$s$)\backslash \backslash$

$\backslash$hline Launch & $0$ & $0\backslash \backslash$

$\backslash$hline Begin roll maneuver & $10$ & $185\backslash \backslash$

$\backslash$hline End roll maneuver & $15$ & $319\backslash \backslash$

$\backslash$hline Throttle to $89\backslash \%$ & $20$ & $452\backslash \backslash$

$\backslash$hline Throttle to $67\backslash \%$ & $32$ & $742\backslash \backslash$

$\backslash$hline Throttle to $104\backslash \%$ & $59$ & $1,315\backslash \backslash$

$\backslash$hline Maximum dynamic pressure & $62$ & $1,430\backslash \backslash$

$\backslash$hline Solid rocket booster separation & $125$ & $4,131\backslash \backslash$

$\backslash$hline

$\backslash$end$\{$tabular$\}$

Use a right Riemann sum with six intervals indicated in the table to estimate the height $\backslash ($ h $\backslash )($in ft$),$ above the earth's surface of the space shuttle, $62$ seconds after liftoff. $($Give the upper approximation available from the data.$)$

$\backslash ($ h$=\backslash )\backslash (\backslash$square $\backslash )$