Question: Which of the following R code generates a 40 row by 4 column design matrix, which has ones in its first column and its remaining

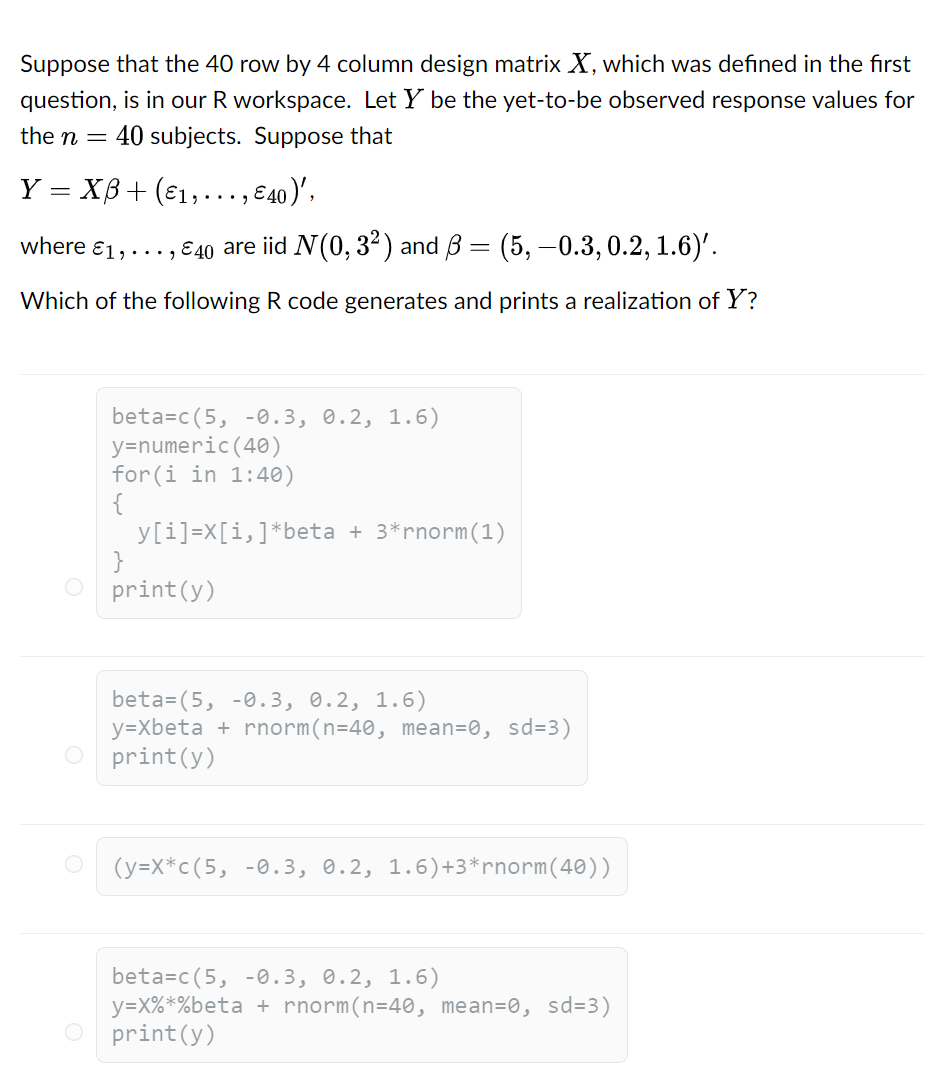
![in X? X=matrix(NA, nrow=40, ncol=4) O X[, 1 ]=rep(1, 40) O X=matrix(rnorm(40*4)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667cce97a1a0e_383667cce97867aa.jpg)

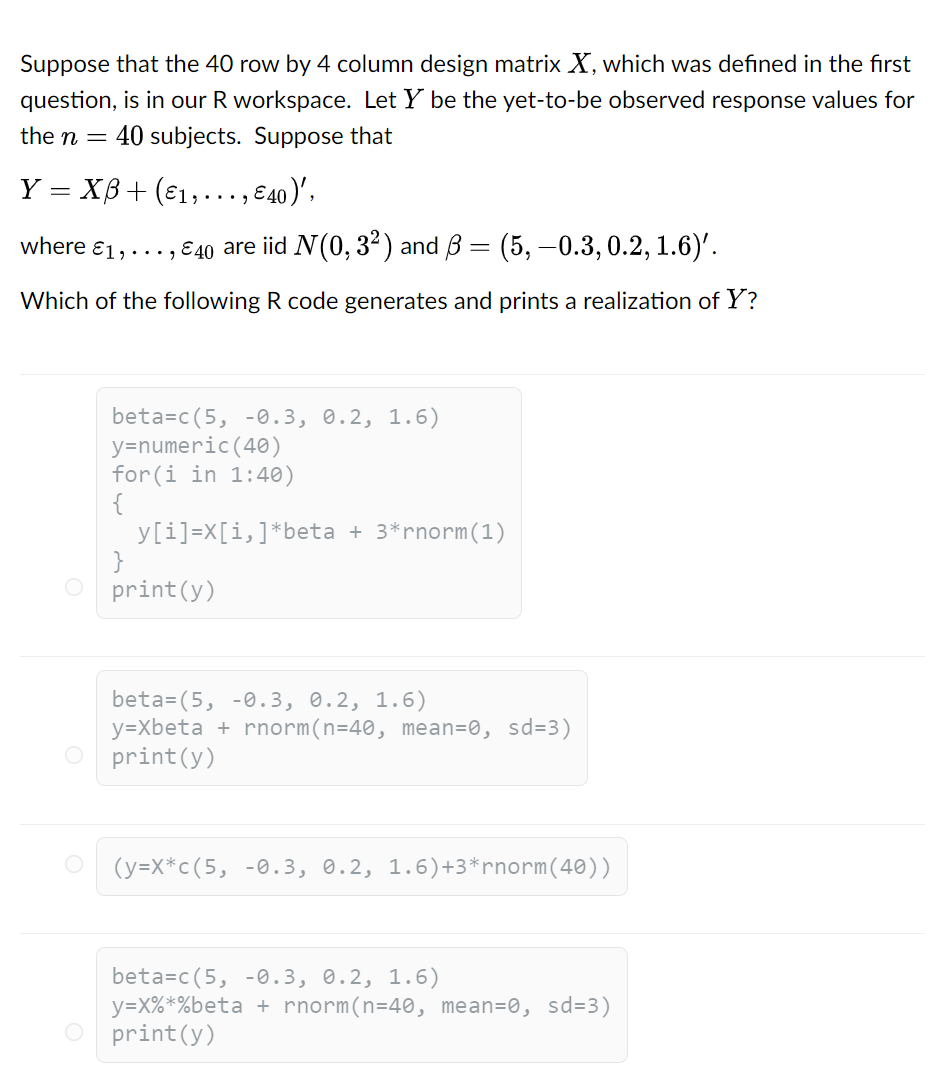
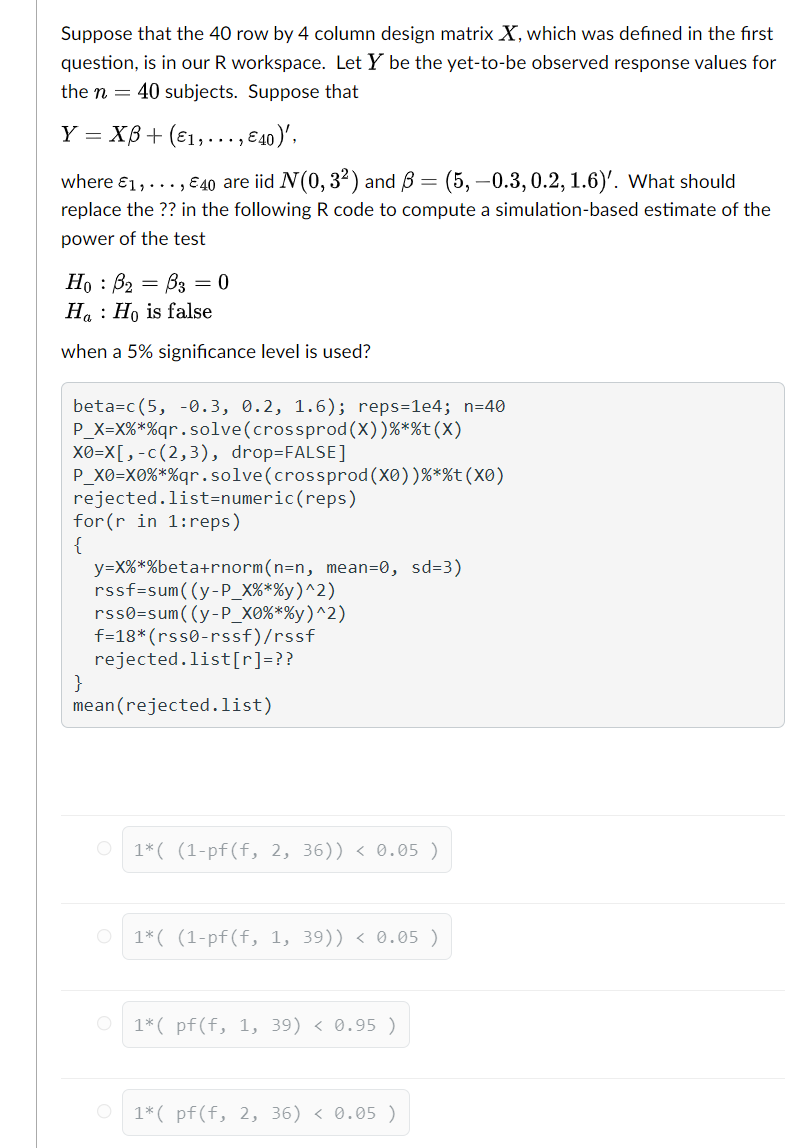

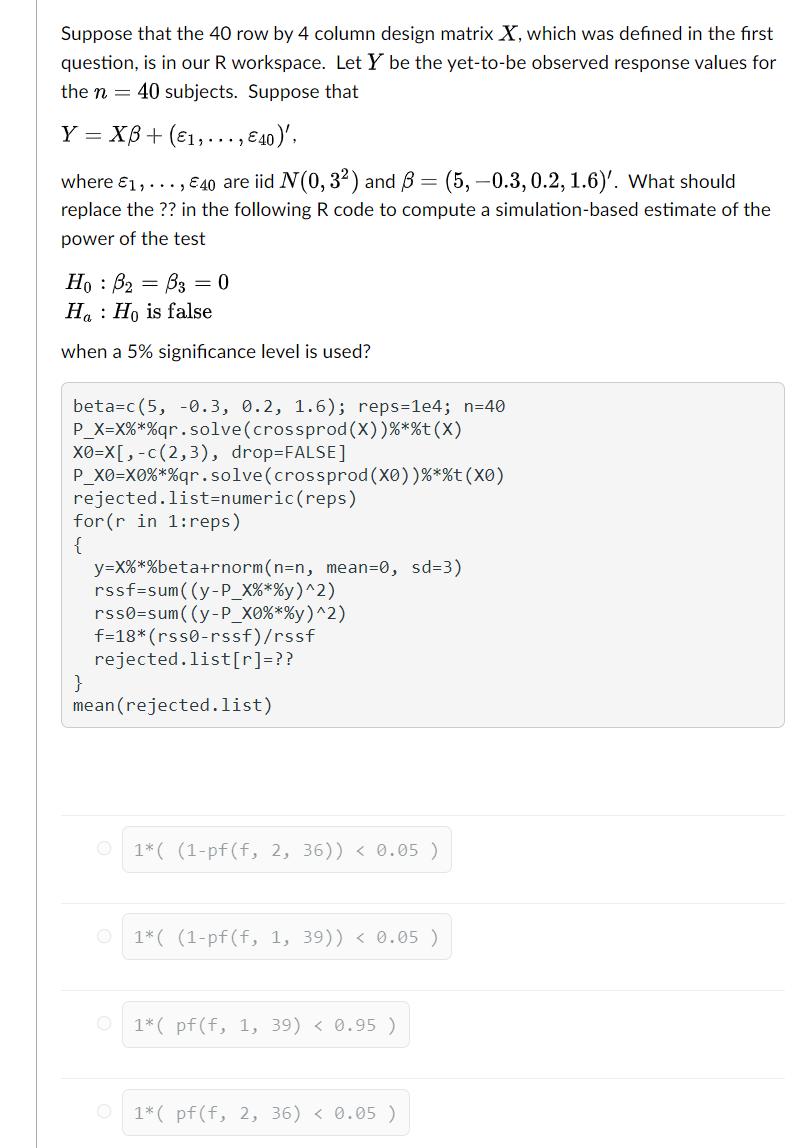
Which of the following R code generates a 40 row by 4 column design matrix, which has ones in its first column and its remaining entries are independently drawn from N(0, 1), and stores it in X? X=matrix(NA, nrow=40, ncol=4) O X[, 1 ]=rep(1, 40) O X=matrix(rnorm(40*4) , nrow=40, ncol=4) O X=cbind(1, matrix(rnorm(40), now=40, ncol=3) ) O X=cbind(1, matrix(rnorm(40*3) , nrow=40, ncol=3) )Suppose that the 40 row by 4 column design matrix X, which was defined in the first question, is in our R workspace. Let Y be the yet-to-be observed response values for the n = 40 subjects. Suppose that Y = XB+ (81, . . ., 840)', where E1, . . ., E40 are iid NV(0, 32 ) and B = (5, -0.3, 0.2, 1.6)'. Which of the following R code generates and prints a realization of Y? beta=c (5, -0.3, 0.2, 1.6) y=numeric (40) for(i in 1:40) y[i]=X[i, ]*beta + 3*rnorm(1) O print (y ) beta= (5, -0.3, 0.2, 1.6) y=Xbeta + rnorm(n=40, mean=0, sd=3) O print (y) O (y=X*c(5, - 0. 3, 0.2, 1.6)+3*rnorm(40) ) beta=c (5, -0.3, 0.2, 1.6) y=X%*%beta + rnorm(n=40, mean=0, sd=3) O print (y)Suppose that the 40 row by 4 column design matrix X, which was defined in the first question, is in our R workspace. Let Y be the yet-to-be observed response values for the n = 40 subjects. Suppose that Y = XB+ (81 , . . ., 840)' , where 61, . . ., 840 are iid IV(0, 32 ) and B = (5, -0.3, 0.2, 1.6)'. What should replace the ?? in the following R code to compute a simulation-based estimate of the power of the test Ho : B2 = B3 = 0 Ha : Ho is false when a 5% significance level is used? beta=c (5, -0.3, 0.2, 1.6); reps=1e4; n=40 P X=XX*%qr . solve(crossprod(X) )%*%t(X) XO=X[, -c(2,3), drop=FALSE] P_XO=X0%*%qr . solve(crossprod (X0) )%*%t (X0) rejected. list=numeric(reps) for(r in 1: reps) { y=XX*%beta+rnorm(n=n, mean=0, sd=3) rssf=sum( (y-P_xx*%y)^2) rss0=sum( (y-P_x0%*%y) ^2) f=18*(rss0-rssf)/rssf rejected. list [r ]=?? } mean (rejected. list) O 1 * ( (1 -pf (f , 2, 36 ) )
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


