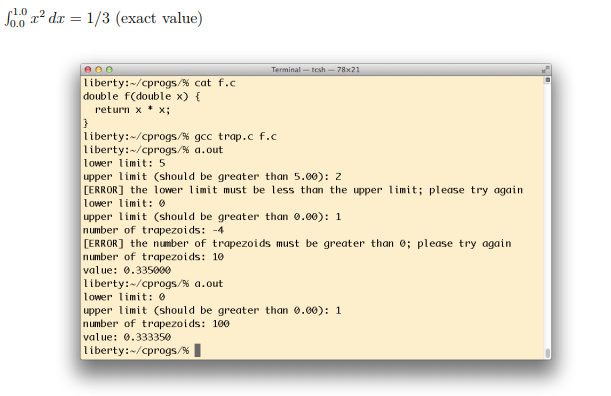
Write a complete C program that inputs values a, b, and n and then outputs (without formatting, i.e. using printf format string "%lf") the sum of the areas of the n trapezoids. You must use the trapezoidal rule to perform your integration by defining and calling a function you write called trap with the signature double trap(double a, double b, int n) (where a, b, and n correspond to the values mentioned in the example above). Your program should check for and only allow correct values to be passed to trap (i.e. b must be greater than a, and n must be greater than 0). Print an appropriate error message and force them to try again if the user does not provide correct input (see the sample run below). All floating point values should be inputted and stored as type double. Your trap function cannot access any global variables of any kind! Your function (i.e. f(x) in the example above) must have signature double f(double x) and be placed in a different file (suggested name of file: f.c, though any name is OK) than the file containing your main function. File f.c will be compiled separately as I demonstrated in class (see the appendix); you should not turn in this file as I will use my own to test your code (i.e. I will provide my own function f(x) in a separate file when I run your project code). Note that this function (i.e. f(x)) should be directly accessed (called) from your function trap.

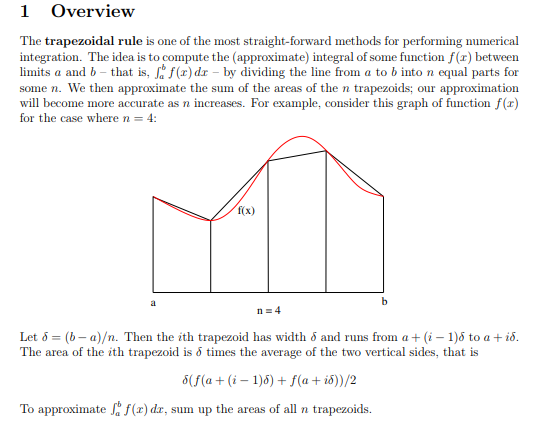
1 Overview The trapezoidal rule is one of the most straight-forward methods for performing numerical limits a and b _ that is, f(r)dr-by dividing the line from a to b into n equal parts for some n. We then approximate the sum of the areas of the n trapezoids; our approximation will become more accurate as n increases. For example, consider this graph of function f() for the case where n 4: f(x) Let ?-(b-a). Then the ith trapezoid has width ? and runs from a + (i-1)s to a + i6. The area of the ith trapezoid is ? times the average of the two vertical sides, that is To approximate J f(x) dr, sum up the areas of all n trapezoids