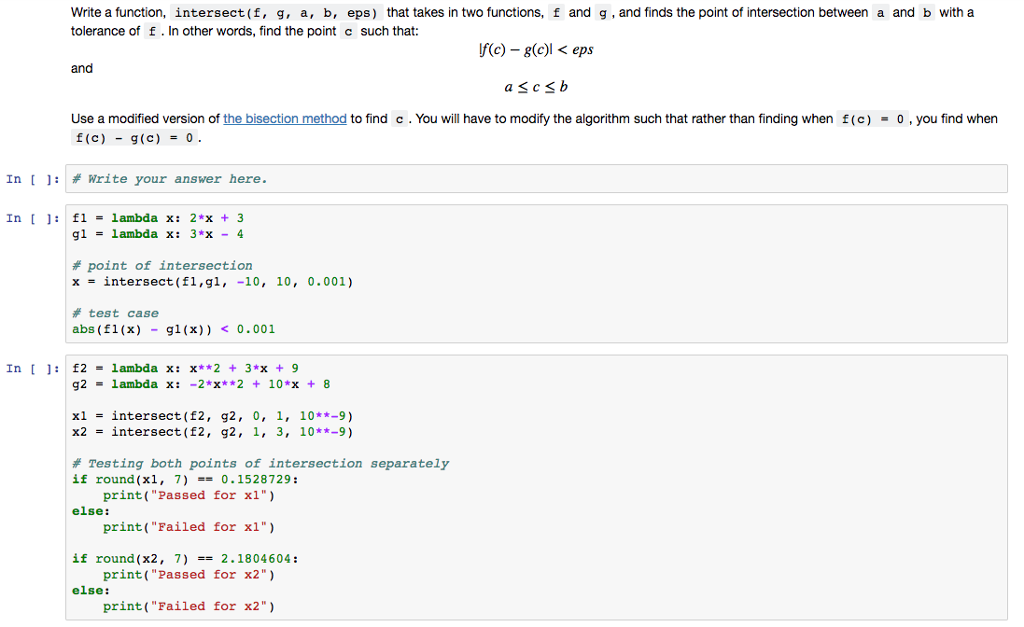
Write a function, intersect(f, g, a, b, eps) that takes in two functions, f and g, and finds the point of intersection between a and b with a tolerance of f. In other words, find the point c such that: f(c) g(c)l eps and Use a modified version of the bisection method to find c. You will have to modify the algorithm such that rather than finding when f (c)0, you find when f(c) -g(c) = 0 In [ ]: # Write your answer here. In fl -lambda x: 2*x +3 gl = lambda x: 3"X - 4 # point of intersection x intersect ( fl , gl, -10, 10, 0.001) # test case abs (f1 (x)gl (x))