Write a matlab for Gauss elimination using complete pivoting.

Below is the code for partial pivoting...so following the same format and method (ie: adding to the existing code), what would be the code for complete pivoting based on the definition provided?

Definition: "Before each row is normalized, it is advantageous to determine the coefficient with the largest absolute value in the column below the pivot element. The rows can then be switched so that the largest element is the pivot element. This is called partial pivoting. If columns as well as rows are searched for the largest element and then switched, the procedure is called complete pivoting"

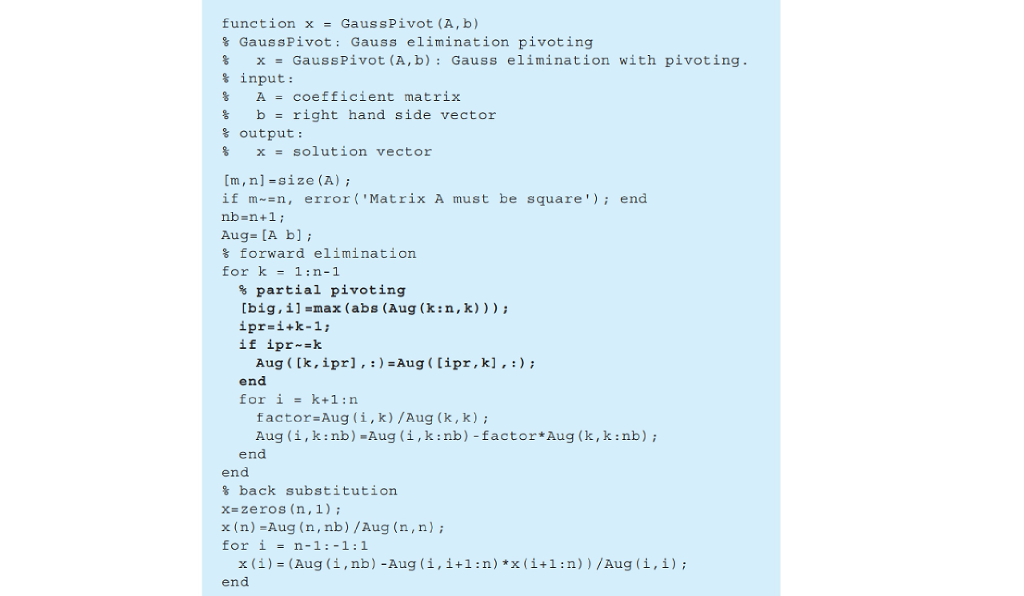
Editable Code:

function x = GaussPivot(A,b)

% GaussPivot: Gauss elimination pivoting

% x = GaussPivot(A,b): Gauss elimination with pivoting.

% input:

% A = coefficient matrix

% b = right hand side vector

% output:

% x = solution vector

[m,n]=size(A);

if m~=n, error('Matrix A must be square'); end

nb=n+1;

Aug=[A b];

% forward elimination

for k = 1:n-1

% partial pivoting

[big,i]=max(abs(Aug(k:n,k)));

ipr=i+k-1;

if ipr~=k

Aug([k,ipr],:)=Aug([ipr,k],:);

end

for i = k+1:n

factor=Aug(i,k)/Aug(k,k);

Aug(i,k:nb)=Aug(i,k:nb)-factor*Aug(k,k:nb);

end

end

% back substitution

x=zeros(n,1);

x(n)=Aug(n,nb)/Aug(n,n);

for i = n-1:-1:1

x(i)=(Aug(i,nb)-Aug(i,i+1:n)*x(i+1:n))/Aug(i,i);

end

function x GaussPivot (A, b) % GaussPivot: Gauss elimination pivoting x Ga u s s Pivot (A, b) : Gauss elimination with pivoting. % input: A = coefficient matrix b = right hand side vector % output: x solution vector [m, n] size (A) If m~=n, error ("Matrix A must be square'); end nb-n+1; Aug- [A b]; % forward elimination for k -1:n-1 % partial pivoting big,i]-max (abs (Aug (k:n,k))) ipr-i+k-1 if ipr-k Aug ( [k, ipr) , : ) =Aug ( [ipr, k] , : ) ; end for i k+1 : n factor=Aug ( , k) /Aug (k, k) ; Aug (i.k:nb)-Aug (i.k:nb)-factor*Aug (k,k:nb ) ; end end % back substitution x= zeros (n, 1) ; x (n) -Aug (n, nb) /Aug (n, n) for i n-1:-1:1 x (i) (Aug (i, nb) -Aug (i,i+1:n)*x (i+1:n))/Aug (i,i); end