1. Write a recursive method called pi_approximation(n) that calculates the Leibniz approximation of given below. Note that you will need to multiply the result by 4 to get the approximation of .

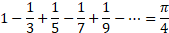
Note that the n^th term can be calculated as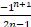

2. Write a recursive method called lengthOfLongestSubsequence(a, b) that calculates the length of the longest common subsequence (lcs) of two strings. For example, given the two strings aaacommonbbb and xxxcommonzzz the lcs is common which is 6 characters long so your function would return 6. The length of the lcs of two strings a & b can be calculated as follows:

0 if the length of a or b is 0

1 + lcs(a[1-], b[1-]) if a[0]=b[0]

max(lcs(a,b[1-]), lcs(a[1-],b)) in all other cases

where a[1-] is the string with the first character removed. You only need to return the length of the longest common subsequence. You do not need to find the longest common sequence.

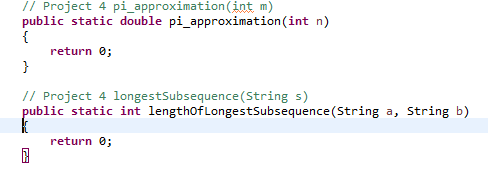
// Project 4 pi_approximation (int m) public static double pi_approximation(int n) return ; // Project 4 longestSubsequence (String s) public static int lengthof LongestSubsequence(String a, String b) return