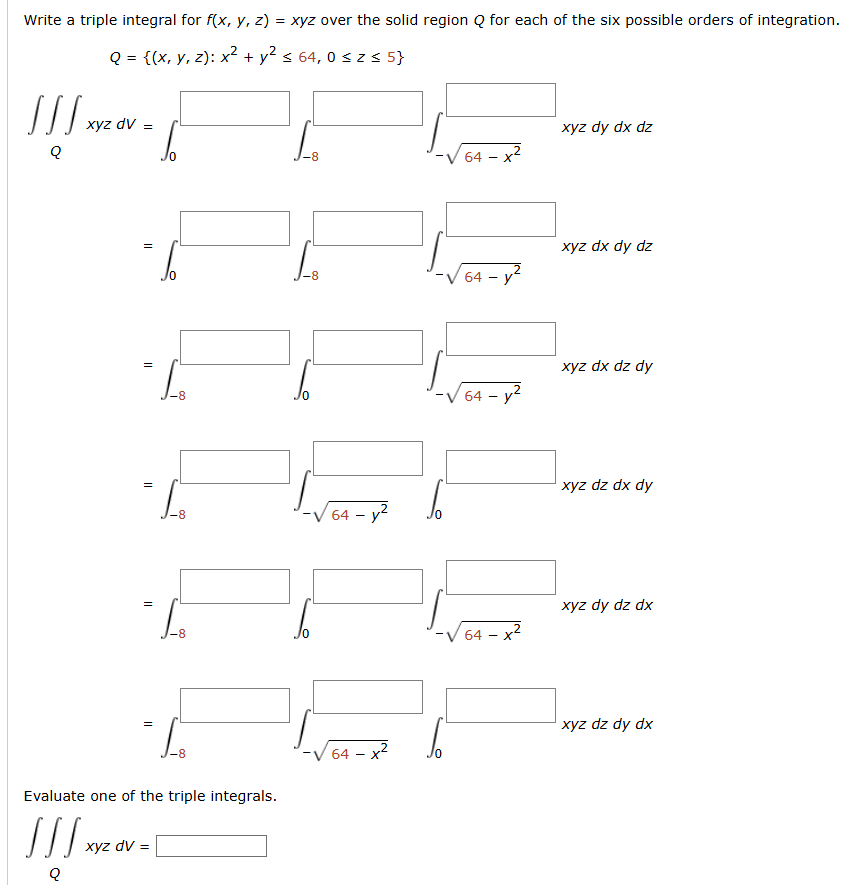
Question: Write a triple integral for f ( x , y , z ) = xyz over the solid region Q for each of the six

Write a triple integral for f(x,y,z)=xyz over the solid region Q for each of the six possible orders of integration.
Q={(x,y,z):x^(2)+y^(2)=64,0=z=5}
_(Q)xyzdv=\int_0\int_(-\sqrt(64-x^(2))) xyzdydxdz
=\int_0\int_(-8)\int_(-\sqrt(64-y^(2))) xyzdxdydz
=\int_(-8)\int_(-\sqrt(64-y^(2))) xyzdxdzdy
=\int_(-8)^\int_(-\sqrt(64-y^(2)))\int_0 xyzdzdxdy
=\int_(-8)\int_(-\sqrt(64-x^(2))) xyzdydzdx
=\int_(-8)\int_(-\sqrt(64-x^(2))) xyzdzdydx
Evaluate one of the triple integrals.
_(Q)xyzdv=
Write a triple integral for f ( x , y , z ) = xyz

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

I need help Homework8: Problem 2 Previous Problem Problem List Next Problem (1 point) Find the limits of integration ly, uy, Ix, ux, Iz, uz (some of which will involve variables x, y, z) so that Sit...

Q:

1.Consider the solid tetrahedron E with vertices O (0,0,0), A (7,0,0), B (0,7,0), and C (0,0,7) . (a) (1 pt.) Sketch the solid E in the xyz -space. Clearly label the axes and all the relevant points...

Q:

1.Consider the solid tetrahedron E with vertices O (0,0,0), A (7,0,0), B (0,7,0), and C (0,0,7) . (a) (1 pt.) Sketch the solid E in the xyz -space. Clearly label the axes and all the relevant points...

Q:

4 x 1 Let f(x) = + 2 and let R be the region bounded by the graph of f and the xaxis on the B 16x 2 interval [1, 3]. a. Find the area of the surface generated when the graph of f on [1, 3] is...

Q:

Calculus What does the following double integral calculate? 1 1 , f( x, v)dA mass of a solid none of these above O area of the region D volume of a solid bounded by the surface S over a region D D...

Q:

8. [0/1 Points] PREVIOUS ANSWERS SCALCET9 15.4.032. ASK YOUR TEACHER PRACTICE ANOTHER (a) A lamp has two bulbs, each of a type with average lifetime 1,700 hours. Assuming that we can model the...

Q:

solve 5.) Write a triple iterated integral for at, y, z) = xyz over the solid region Q for each of the six possible orders of integration. Q{(x,y,z)|0$xs1,05y51x2,OSzS6} 6.) Find the mass and the...

Q:

3. Let f(x, y, z) = x(1 x y 2), where s 0 is a parameter. a) [3 marks] Sketch the region of integration for the following triple integral, [ [ [ f (x, y, z) dV = SS S = S. So 1 1-x 1-x-y f(x, y, z)...

Q:

Calculus 3: 15.3Tripleintegrals Show Work 1. Evaluate [IS(6xy + 22)dV, where B = [-4, 4] x [0, 1] x [0, 4] (Use symbolic notation and fractions where needed.) SSB(6xy + =2) dV =Evaluate [ISg f(x, y,...

Q:

1. [-/1 Points] DETAILS LARCALC11 14.2.010. Sketch the region R and evaluate the iterated integral / / Rx. ") ca. 10 2 - X 6 8 10 -1 2 3 O 10 4 10 8 8 6 21 2 3 1 / R( x , V ) dA = [2. [-/1 Points]...

Q:

A swimming pool can be filled in 11 hours if water enters through a pipe alone, or in 20 hours if water enters through a hose alone. If water is entering through both the pipe and the hose, how long...

Q:

Storrer Co. identifies the following activities that pertain to manufacturing overhead: materials handling, machine setups, factory machine maintenance, factory supervision, and quality control. For...

Q:

Everyone who can benefit from refinancing in the U . S . always exercises this option Question 7 options: TrueFalse

Q:

What are some food related health care issues that inner cities are more likely to see than more affluent areas? Why are certain areas most likely to experience inadequate healthy food options than...