write in python and give me the code. thx

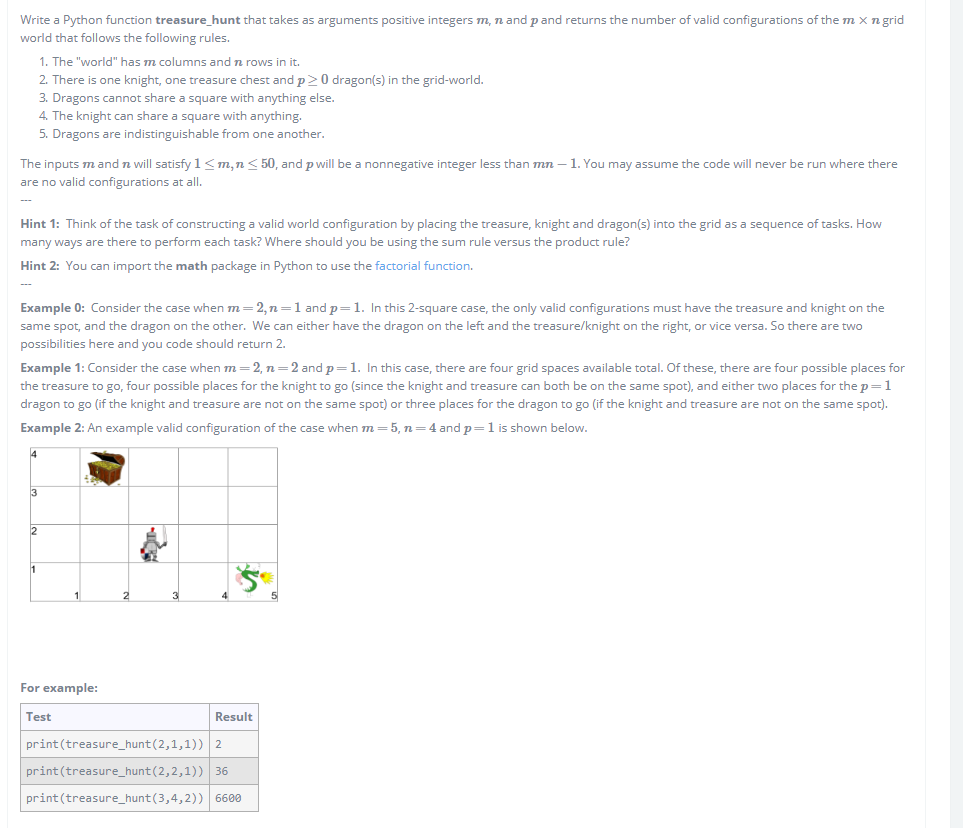
Write a Python function treasure hunt that takes as arguments positive integers m, n and pand returns the number of valid configurations of the m X n grid world that follows the following rules. 1. The "world" has m columns and n rows in it. 2. There is one knight, one treasure chest and p 0 dragon(s) in the grid-world. 3. Dragons cannot share a square with anything else 4. The knight can share a square with anything. 5. Dragons are indistinguishable from one another The inputs m and n will satisfy 1 Sm,n are no valid configurations at all. 50, and p will be a nonnegative integer less than mn-1.You may assume the code will never be run where there Hint 1: Think of the task of constructing a valid world configuration by placing the treasure, knight and dragon(s) into the grid as a sequence of tasks. How many ways are there to perform each task? Where should you be using the sum rule versus the product rule? Hint 2: You can import the math package in Python to use the factorial function. Example 0: Consider the case when m = 2, n-1 and P-1. In this 2-square case, the only valid configurations must have the treasure and knight on the same spot, and the dragon on the other. We can either have the dragon on the left and the treasure/knight on the right, or vice versa. So there are two possibilities here and you code should return 2. Example 1: Consider the case when m = 2, n = 2 and P = 1. In this case, there are four grid spaces available total. Of these, there are four possible places for the treasure to go, four possible places for the knight to go (since the knight and treasure can both be on the same spot), and either two places for the p = 1 dragon to go (if the knight and treasure are not on the same spot) or three places for the dragon to go (if the knight and treasure are not on the same spot). Example 2: An example valid configuration of the case when m = 5, n = 4 and p = 1 is shown below For example Test print (treasure_hunt (2,1,1)) 2 print(treasure_hunt (2,2,1)) 36 print (treasure_hunt(3,4,2)) 6600 Result Write a Python function treasure hunt that takes as arguments positive integers m, n and pand returns the number of valid configurations of the m X n grid world that follows the following rules. 1. The "world" has m columns and n rows in it. 2. There is one knight, one treasure chest and p 0 dragon(s) in the grid-world. 3. Dragons cannot share a square with anything else 4. The knight can share a square with anything. 5. Dragons are indistinguishable from one another The inputs m and n will satisfy 1 Sm,n are no valid configurations at all. 50, and p will be a nonnegative integer less than mn-1.You may assume the code will never be run where there Hint 1: Think of the task of constructing a valid world configuration by placing the treasure, knight and dragon(s) into the grid as a sequence of tasks. How many ways are there to perform each task? Where should you be using the sum rule versus the product rule? Hint 2: You can import the math package in Python to use the factorial function. Example 0: Consider the case when m = 2, n-1 and P-1. In this 2-square case, the only valid configurations must have the treasure and knight on the same spot, and the dragon on the other. We can either have the dragon on the left and the treasure/knight on the right, or vice versa. So there are two possibilities here and you code should return 2. Example 1: Consider the case when m = 2, n = 2 and P = 1. In this case, there are four grid spaces available total. Of these, there are four possible places for the treasure to go, four possible places for the knight to go (since the knight and treasure can both be on the same spot), and either two places for the p = 1 dragon to go (if the knight and treasure are not on the same spot) or three places for the dragon to go (if the knight and treasure are not on the same spot). Example 2: An example valid configuration of the case when m = 5, n = 4 and p = 1 is shown below For example Test print (treasure_hunt (2,1,1)) 2 print(treasure_hunt (2,2,1)) 36 print (treasure_hunt(3,4,2)) 6600 Result