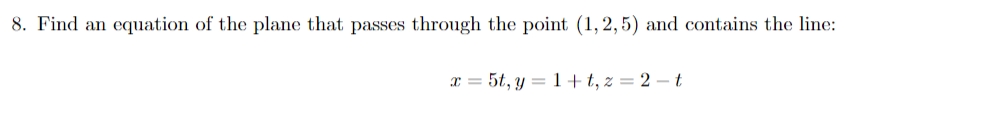
Write the answer SPECIFIC!

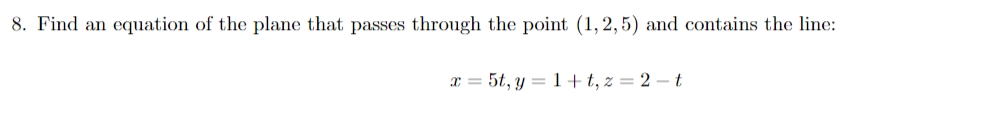
2. Solve all parts. (a) Find the vector equation of a line passing through the point (1, 2, 3) and parallel to a = (1,0, 1). (b) Find the equation of a second line that passes points (1, 5, 7) , (3, ll, 17) (e) Determine if the lines intersect and if yes, nd the point of intersection of the two lines above. 3. Follow the directions below: 1 (a) Write the equation of a plane with normal '5? = (2, 5, 3) and having point P\" (,{}, 5) (b) Determine whether P1 (5,2,9) and P2 (2, 1,5) belong on the plane from (a). (e) Compare the plane you found in (a) with .1: + 4(3) 2) + 6(z 5) = {I do these two surfaces intersect? If yes, at what angle? (d) Find the distance between the plane from part (c) and the origin. 5. Let f(x, y) e -( TV ) . (a) Describe the domain of f(x, y). (c) By computing the partial derivatives and substituting show that f(x, y) satisfies the heat equation: of a2 f ay6. Consider the sphere given by: 3:2 + y2 + 2:2 89: + 21; 62: + 25 = i} (a) Find the center and radius of this sphere. (b) Find the distance between the center and the origin. (c) Find the distance between the sphere and the origin. ((1) Describe the intersection of this sphere with the three coordinate planes (icy1 3'2 and X2 planes]. 8. Find an equation of the plane that puma through the point (1, 2, 5} and contains the line: m=5t,y=1+t,z=2t