Write this Program in C langauge

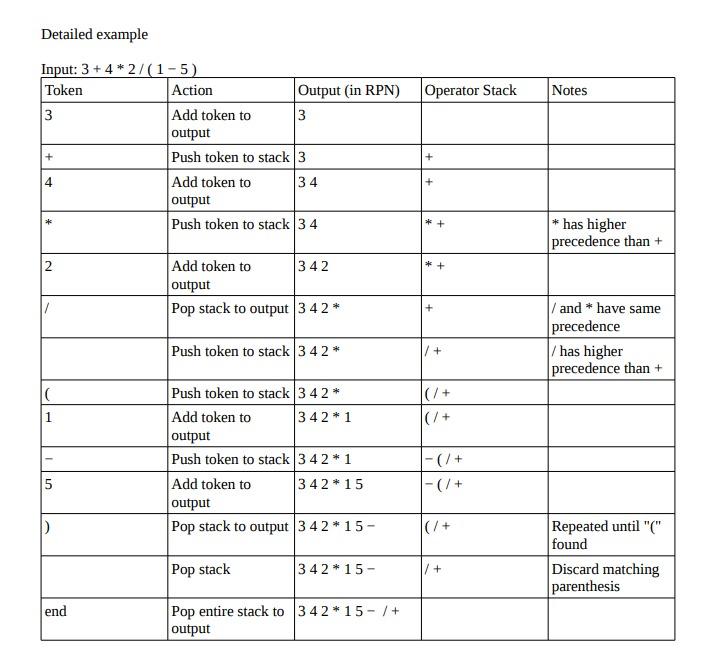
State 0: - Increment index string index - If current input is number, next state is 1 - If current input is operator, next state is 2 - If current input is ieft parenthesis, next state is 3 - If current input is right parenthesis, next state is 4 - If current input is end of string, nent state is 5 - If cument input is garbage, next state is 6 State 1: (found number) - Copy current character to output string - Increment output string index - Increment input string index. - While character in input string is digit ar decimal point - Copy character to output string - Increment output string index - increment input string index - Put space in output string - Increment output string inder - Decrement input string lindex - Neat state is 0 State 2: (found operator) - While the stack is not emply and the character at top of stack is an operator and the precedence of the operator that is curment character in input string is less than or equal to that of the operator on to of the stadk - Pop operator off top of stack and put in output string - Increment output string index - Put space in output string - increment output string index - If stack is not full, Push the operator that is current character in input string an stack Otherwise, print error and exet - Neat state is 0 State 3: (found ieft parenthesis) - It stack is not full, push left parenthess tound in current input character on stack Otherwise, display eror message and evit - Neat state is 0 State 4: (found right parenthesis) - While stack is not empty and item at top of stack is not ieft parenthesis - Pop operator oft top of stack and put in autput string - increment output string index - Put space in output string - Increment output string index - If stack is not empty, pap left parentheses off stop of stack but do not put in output string. Otherwise, display eror mesage (mismatched parenthesik) and ext. - Neat state is 0 State 5: (End of input) - While stack is not empty and character at top of stack is an operator - Pop operator off stadk and put in output string - increment output string index - Put space in output string - Increment output string index - If stack is not empty, display error message (leftover parenthess) and exit Otherwise, put end of string marker in output string and send output string ta RPN Evaluator Note: return renevalioutput_stringl; State 6: (garbage) - Display error message and exit Dijkstra's Shunting-Yard Algorithm: NOTE: Modified to include only numbers, operators, and parentheses. - While there are tokens to be read: - Read a token. - If the token is a number, then add it to the output queue. - If the token is an operator, o1, then: - while there is an operator token, o2, at the top of the stack, and o1 is left-associative and its precedence is less than or equal to that of o2. NOTE: Do we need to be concerned about associativity? See note below. - pop 02 off the stack, onto the output queue; - push o1 onto the stack. - If the token is a left parenthesis, then push it onto the stack. - If the token is a right parenthesis: - While the token at the top of the stack is not a left parenthesis - pop operator off the stack onto the output queue. - Pop the left parenthesis from the stack, but not onto the output queue. Note: If the stack runs out without finding a left parenthesis, then there are mismatched parentheses. - When there are no more tokens to read: (ie end of input string) - While there are still operator tokens in the stack: - Pop the operator onto the output queue. Note: If the operator token on the top of the stack is a parenthesis, then there are mismatched parentheses. Note: Associativity is only needed when the operators in an expression have the same precedence. Usually + and - have the same precedence. Consider the expression 74+2. The result could be either: (74)+2=5when+andareleft-associative or 7(4+2)=1when+andareright-associative. Usually the addition, subtraction, multiplication, and division operators are left-associative, while the exponentiation, assignment and conditional operators are right-associative. To prevent cases where operands would be associated with two operators, or no operator at all, operators with the same precedence must have the same associativity. Detailed example