$\{x\},$ overlapping.

Disjoint difference, which returns rectangles th$$t are disjoint.

$$ Largest$-$Cover Difference

Given two rectangles $R=(I_1,I_2,$dots,$I_n)$ and $T=(J_1,J_2,$dots,$J_n),$ their difference $R-T$ is the region $=$tilde$\frac{R}{\frac{?}{?}}$tilde$(T).$ We make the following observation: for a point to be in $R$ and not in $T,$ all it takes is that in one of the dimensions $k,$ it is in $I_k,$ but not in $J_k.$

Based on this idea, we construct a representation of tilde$\frac{R}{\frac{?}{?}}$tilde$(T)$ as follows. We initialize the list of result rectangles to be empty. Then, we iterate over all dimensions $k=1,2,$dots,$n,$ and for each dimension $k,$ we construct rectangles with intervals $I_1,$dots,$I_{k-1},I_k-J_k,I_{k+1},$dots,$I_n,$ where $I_k-J_k$ represents interval difference. There can be $0,1,$ or $2$ intervals in $I_k-J_k,$ and correspondingly, $I_1,$dots,$I_{k-1},I_k-J_k,I_{k+1},$dots,$I_n$ will consist of $0,1,$ or $2$ rectangles; we add all such rectangles to the result list. Let's translate this idea into code.

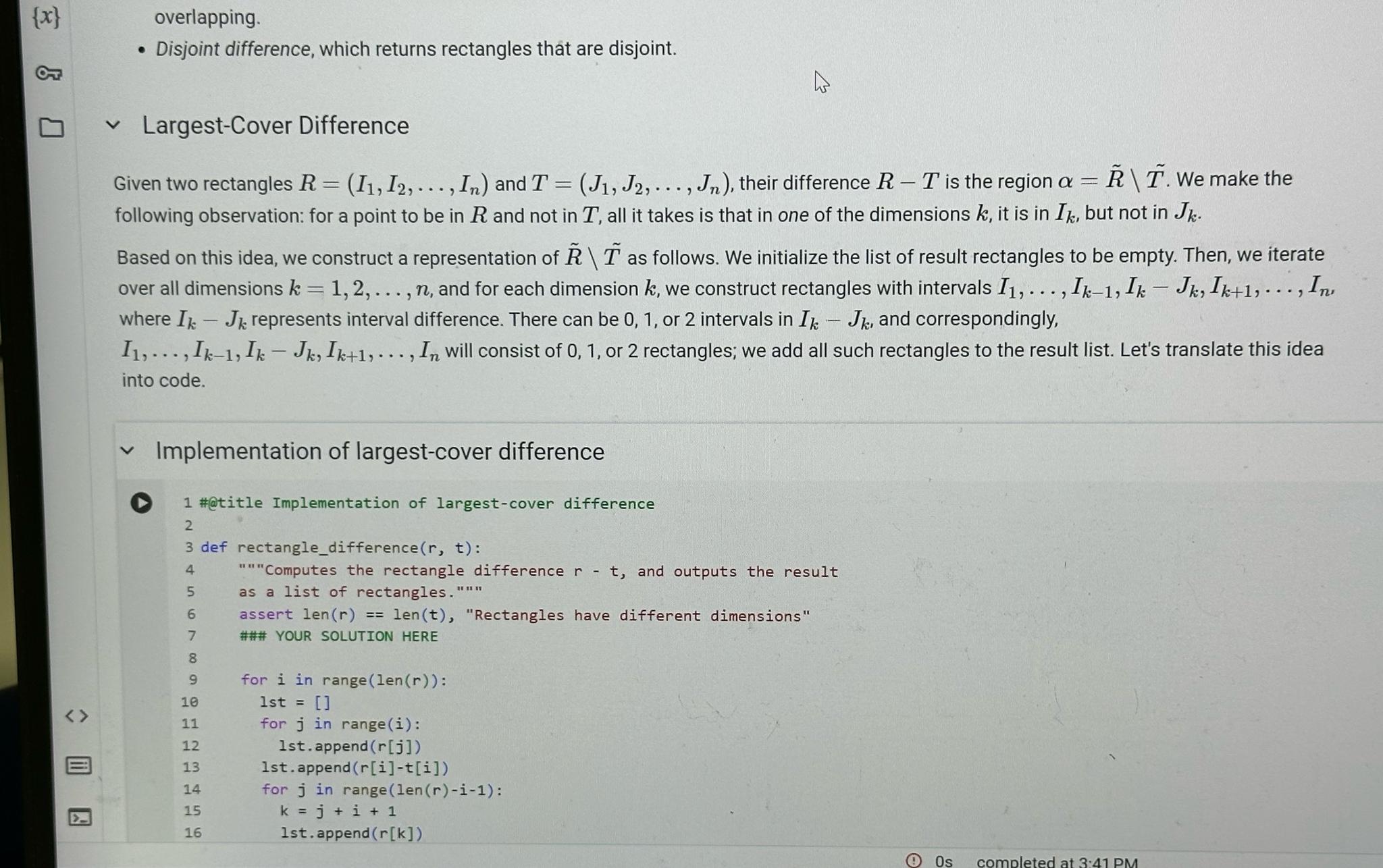
$$ Implementation of largest$-$cover difference

$1$ #@title Implementation of largest$-$cover difference

def rectangle$\_$difference $(r,t)$ :

$"""$Computes the rectangle difference $r-t,$ and outputs the result

as a list of rectangles." $"$n$"$

assert len$(r)==$ len$(t,$ "Rectangles have different dimensions"

### YOUR SOLUTION HERE

for $i$ in range$($len$(r$ :

lst $=[]$

for $j$ in range$($i$)$:

Ist.append $(r[j])$

lst$.$append $($r$[$i$]-$t$[$i$])$

for $j$ in range$($len $(r)-i-1$ :

$k=j+i+1$

$1$st$.$ append $(r[k]$