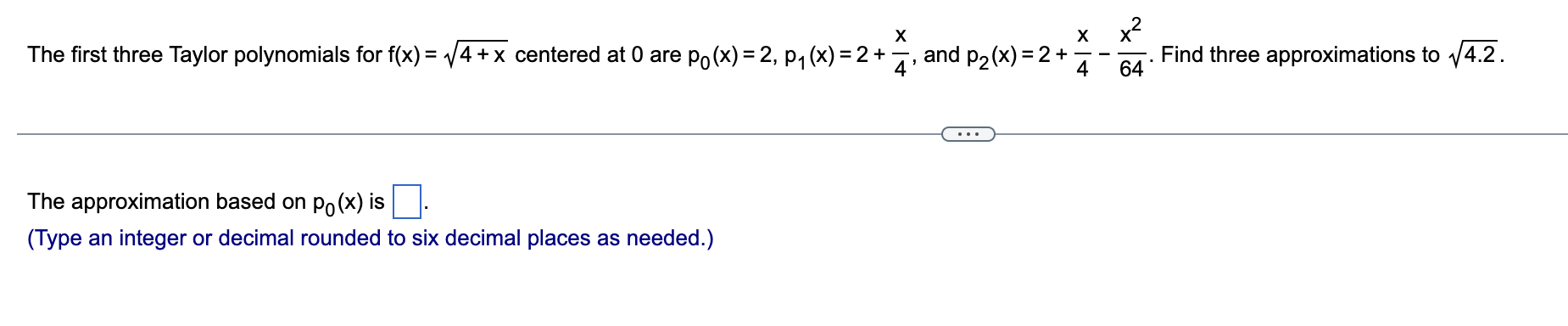
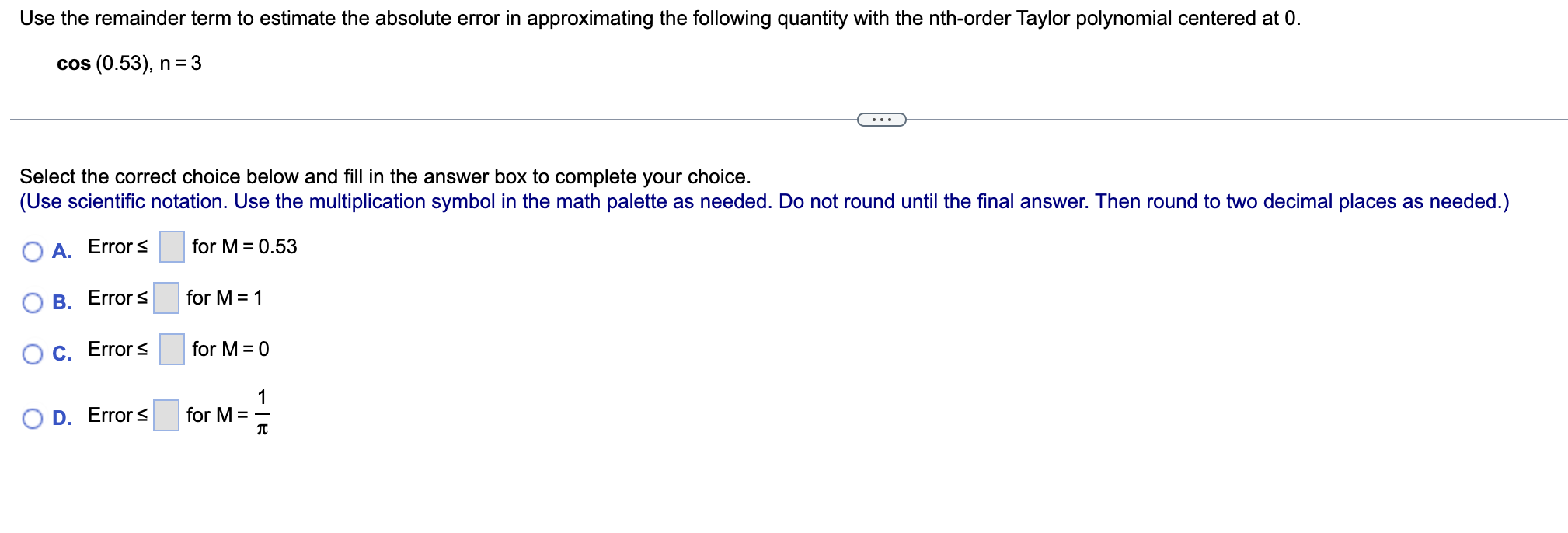
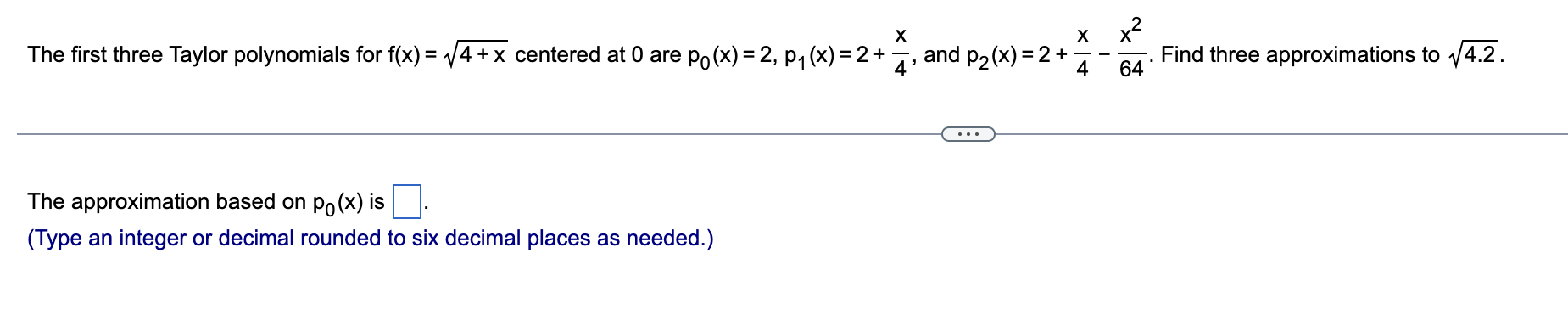
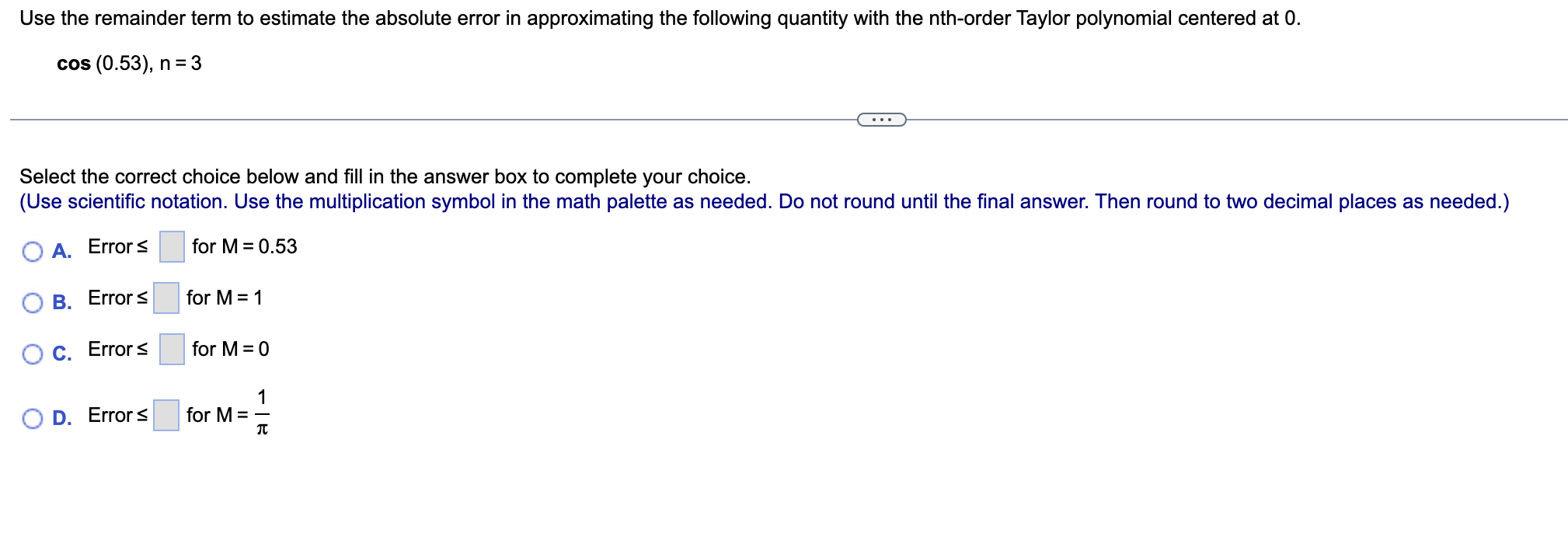
X X X2 The first three Taylor polynomials for f(x) = 1/4 + x centered at 0 are p0(x) = 2, p1(x) = 2 + , and p2(x) = 2 + z - E. Find three approximations to 4.2. E The approximation based on p0(x) is D. (Type an integer or decimal rounded to six decimal places as needed.) Find the Taylor polynomials p, , ..., P; centered at a = 0 for f(x) = 3e-X. P1 ( x ) = a. Use the given Taylor polynomial p2 to approximate the given quantity. b. Compute the absolute error in the approximation assuming the exact value is given by a calculator. 2 x x Approximate 41.04 using f(x) = 1/1 +x and p2(x) =1 + E - F. a. Using the Taylor polynomial p2, 1/104 5 D. (Do not round until the nal answer. Then round to four decimal places as needed.) a. Approximate the given quantity using Taylor polynomials with n = 3. b. Compute the absolute error in the approximation assuming the exact value is given by a calculator. cos(-0.0'l) (E a. p3(-0.01)=|:| (Do not round until the nal answer. Then round to six decimal places as needed.) Use the remainder term to estimate the absolute error in approximating the following quantity with the nthorder Taylor polynomial centered at 0. cos (0.53). n = 3 Select the correct choice below and fill in the answer box to complete your choice. (Use scientific notation. Use the multiplication symbol in the math palette as needed. Do not round until the final answer. Then round to two decimal places as needed.) A. Error 5 for M = 0.53 B. Error 5 for M = 1 c. Error 5 for M = 0 D. Error 5 for M = E What is the minimum order of the Taylor polynomial centered at 0 for cos x required to approximate the following quantity with an absolute error no greater than 10 5'? cos ( - 0.56) The minimum order of the Taylor polynomial is n = |