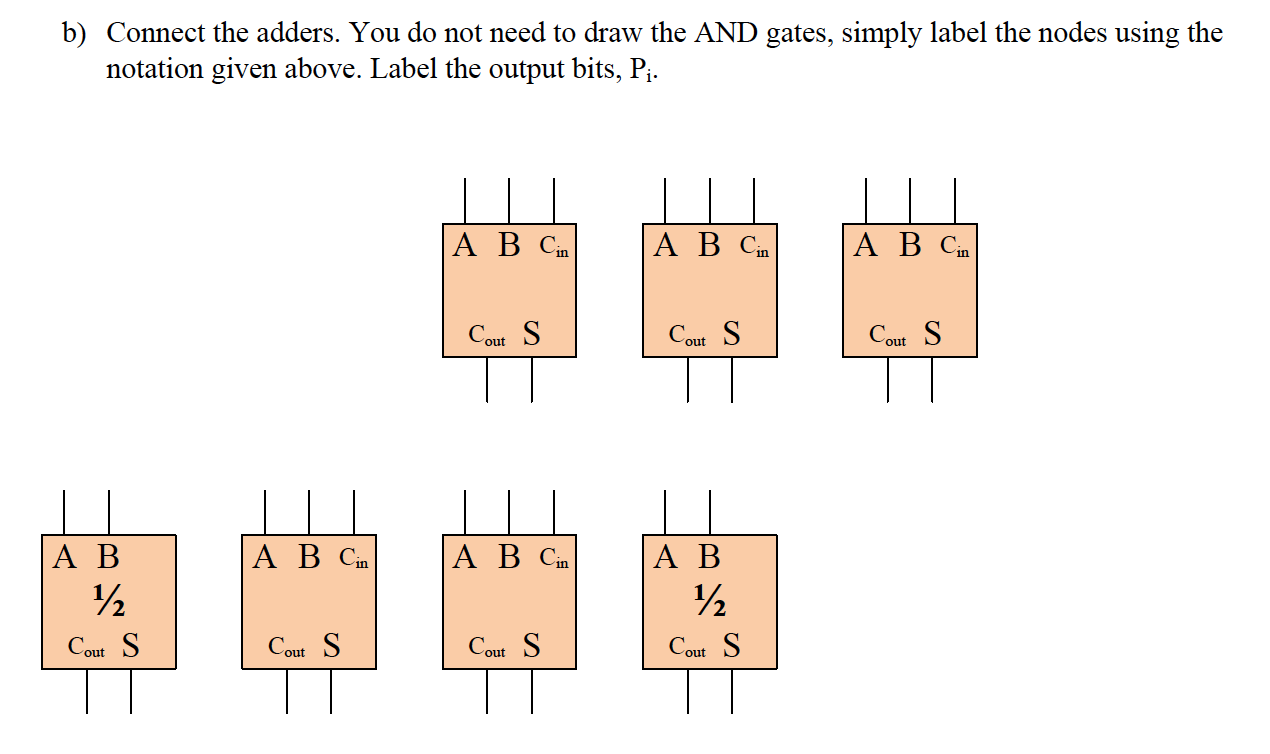
(X+1)?: Design a combinational circuit that computes P = (X+1) = X + 2X+1 The input X is a 4-bit unsigned integer. The output P is an 8-bit unsigned integer. Your design should use a carry-save tree using half and full adders and a ripple adder using half and full adders. a) Show how partial sums are formed from the input bits, Xi. Simplify using the following identities. aba = ab abq = ab a1= use the notation (ij)denote X;X, where i, j e{0, 1, 2, 3} for example (32) denotes XzX, al= a b) Connect the adders. You do not need to draw the AND gates, simply label the nodes using the notation given above. Label the output bits, Pi. A B C CODE S | Cour S Cour S A B Cin | A B Can | 1/2 Cout S 1/2 Cout Cout S Cout S (X+1)?: Design a combinational circuit that computes P = (X+1) = X + 2X+1 The input X is a 4-bit unsigned integer. The output P is an 8-bit unsigned integer. Your design should use a carry-save tree using half and full adders and a ripple adder using half and full adders. a) Show how partial sums are formed from the input bits, Xi. Simplify using the following identities. aba = ab abq = ab a1= use the notation (ij)denote X;X, where i, j e{0, 1, 2, 3} for example (32) denotes XzX, al= a b) Connect the adders. You do not need to draw the AND gates, simply label the nodes using the notation given above. Label the output bits, Pi. A B C CODE S | Cour S Cour S A B Cin | A B Can | 1/2 Cout S 1/2 Cout Cout S Cout S