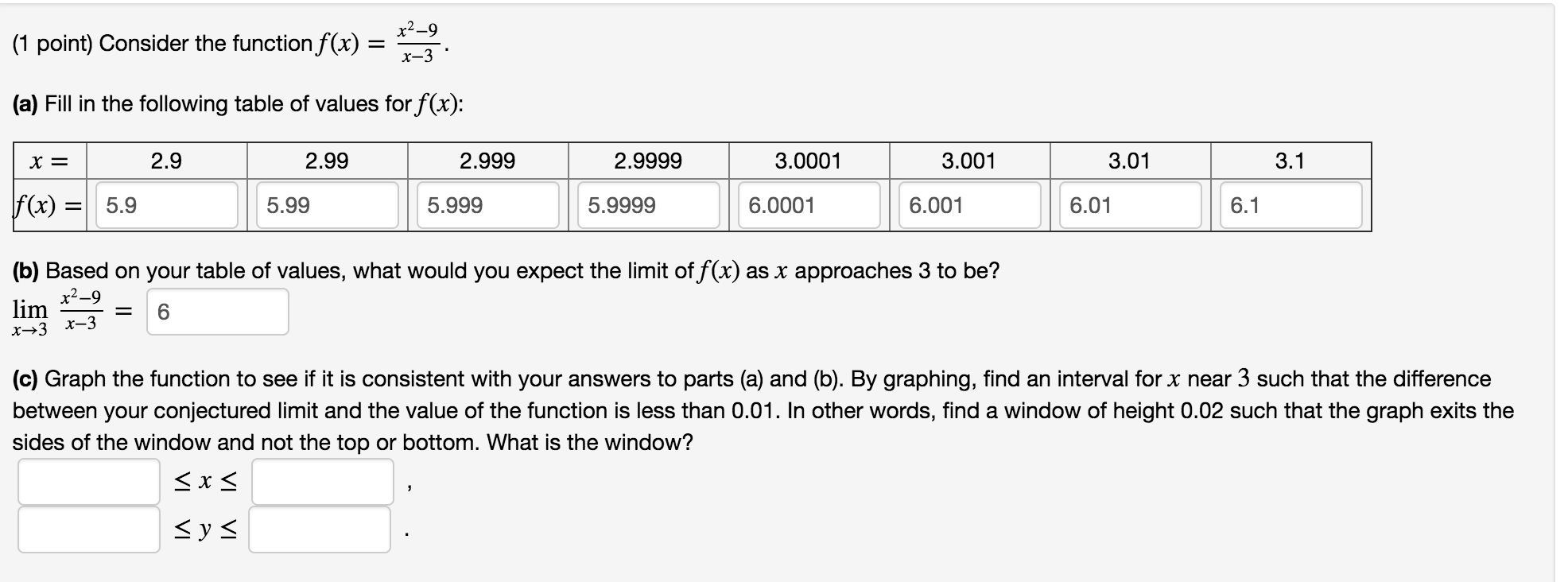
x29 13 ' (1 point) Consider the function f(x) = (3) Fill in the following table of values for f(x): x = 2.9 2.99 2.999 2.9999 3.0001 3.001 3.01 3.1 f(x) = 5.9 5.99 5.999 5.9999 6.0001 6.001 6.01 6.1 (b) Based on your table of values, what would you expect the limit of f(x) as x approaches 3 to be? . 119 _ 3.1331 - 6 (0) Graph the function to see if it is consistent with your answers to parts (a) and (b). By graphing, find an interval for x near 3 such that the difference between your conjectured limit and the value of the function is less than 0.01. In other words, find a window of height 0.02 such that the graph exits the sides of the window and not the top or bottom. What is the window? 5 x 5 5y