yielas two equations:

${}_{x^{\text{'}}}={}_{x}co{s}^2+{}_{y}si{n}^2+{}_{xy}(2sincos)$

${}_{x^{\text{'}}{y}^{\text{'}}}=({}_y-{}_x)sincos+{}_{xy}(co{s}^2-si{n}^2)$

Using the trigonometric identities $2sincos=sin(2),si{n}^2=\frac{1-cos(2)}{2},$ and $co{s}^2=\frac{1+cos(2)}{2}$ and the fact that the $+y^{\text{'}}$ axis is always $90$ counterclockwise from the $+x^{\text{'}}$ axis, we can derive the equations:

${}_{x^{\text{'}}}=\frac{{}_x+{}_y}{2}+\frac{{}_x-{}_y}{2}cos(2)+{}_{xy}sin(2)$

${}_{y^{\text{'}}}=\frac{{}_x+{}_y}{2}-\frac{{}_x-{}_y}{2}cos(2)-{}_{xy}sin(2)$

${}_{x^{\text{'}}{y}^{\text{'}}}=-(\frac{{}_x-{}_y}{2})sin(2)+{}_{xy}cos(2)$

These stress$-$transformation equations allow us to eliminate the geometric work that was involved in the incline$-$plane method of stress transformation and provides us with all three stresses in the primed coordinate system.

In deriving these equations, we have used the standard sign

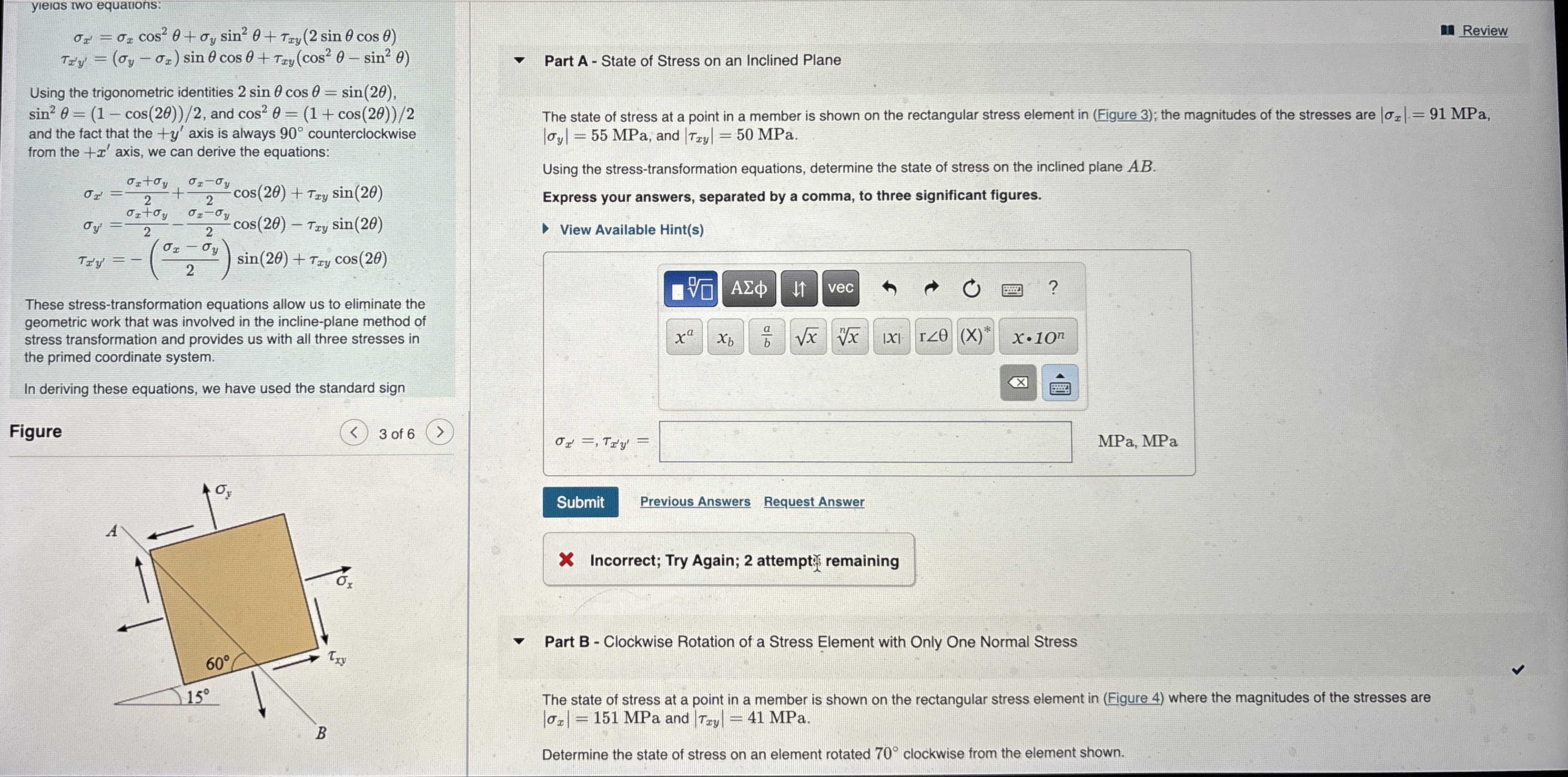
Figure

$3$ of $6$

Part A $-$ State of Stress on an Inclined Plane

The state of stress at a point in a member is shown on the rectangular stress element in $($Figure $3)$; the magnitudes of the stresses are $|{}_x|=91$MPa, $|{}_y|=55$MPa, and $|{}_{xy}|=50$MPa.

Using the stress$-$transformation equations, determine the state of stress on the inclined plane $AB.$

Express your answers, separated by a comma, to three significant figures.

View Available Hint$($s$)$

Previous Answers

Request Answer

Part B $-$ Clockwise Rotation of a Stress Element with Only One Normal Stress

The state of stress at a point in a member is shown on the rectangular stress element in $($Figure $4)$ where the magnitudes of the stresses are $|{}_x|=151$MPa and $|{}_{xy}|=41$MPa.

Determine the state of stress on an element rotated $70$ clockwise from the element shown.