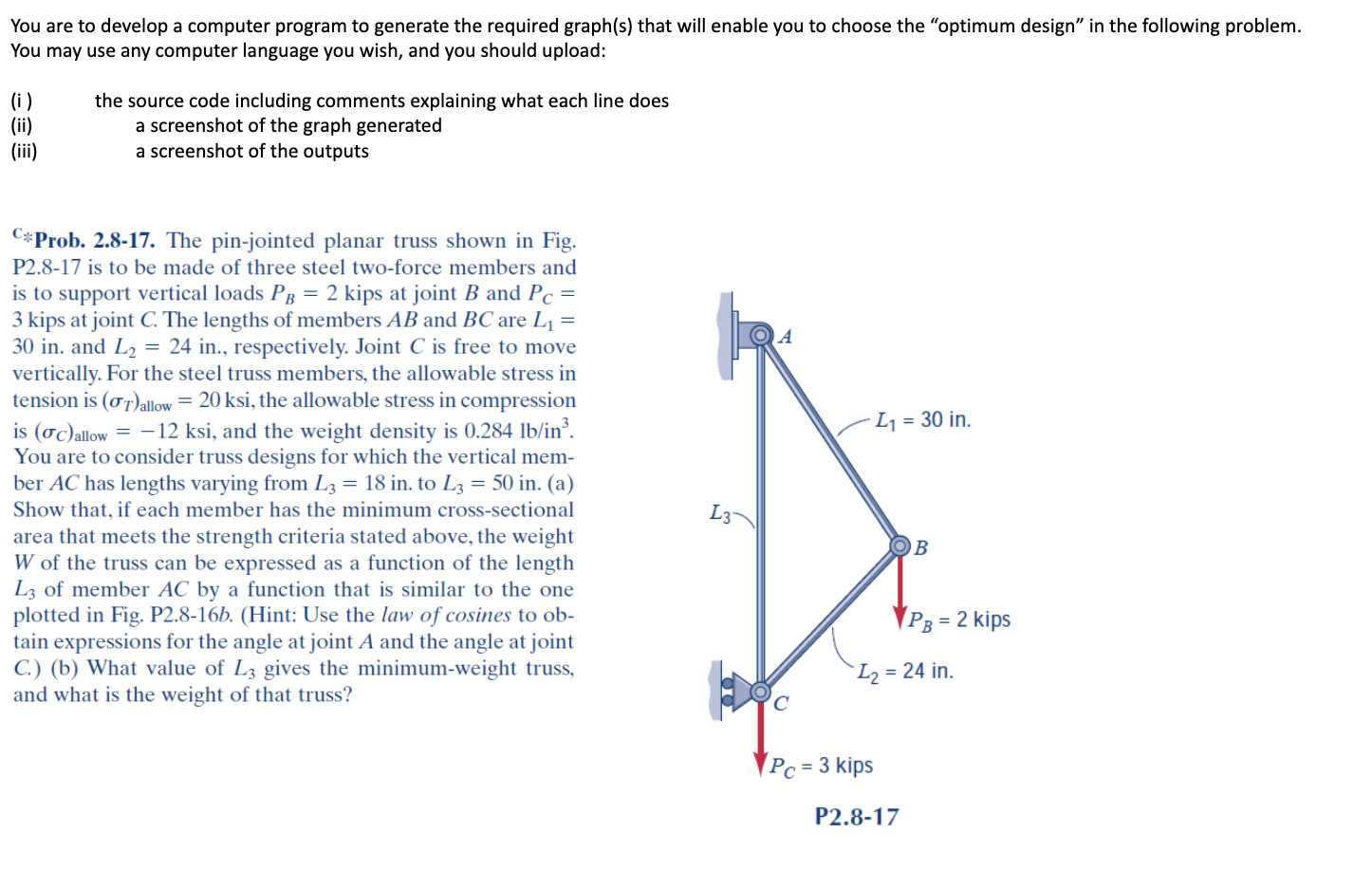
You are to develop a computer program to generate the required graph(s) that will enable you to choose the "optimum design" in the following problem. You may use any computer language you wish, and you should upload: (i) (ii) the source code including comments explaining what each line does a screenshot of the graph generated (iii) a screenshot of the outputs C*Prob. 2.8-17. The pin-jointed planar truss shown in Fig. P2.8-17 is to be made of three steel two-force members and is to support vertical loads PB = 2 kips at joint B and Pc = 3 kips at joint C. The lengths of members AB and BC are L = 30 in. and L2 = 24 in., respectively. Joint C is free to move vertically. For the steel truss members, the allowable stress in tension is (T) allow = 20 ksi, the allowable stress in compression is (c) allow = -12 ksi, and the weight density is 0.284 lb/in. You are to consider truss designs for which the vertical mem- ber AC has lengths varying from L3 = 18 in. to L3 = 50 in. (a) Show that, if each member has the minimum cross-sectional area that meets the strength criteria stated above, the weight W of the truss can be expressed as a function of the length L3 of member AC by a function that is similar to the one plotted in Fig. P2.8-16b. (Hint: Use the law of cosines to ob- tain expressions for the angle at joint A and the angle at joint C.) (b) What value of L3 gives the minimum-weight truss, and what is the weight of that truss? L3 A L = 30 in. B PB = 2 kips L = 24 in. Pc = 3 kips P2.8-17