You must design a cascade compensator to meet the specification for output response to a unit step input, as defined in Table 1. The open loop system you should use for your design should be picked from the row appropriate to your surname 1st initial, as should the overshoot and peak time specifications, and all systems should be designed for zero steady state error.

1.Using the root locus method, as defined in Nises Control System Engineering book (module core book): Chapter 9, Example 9.5, design a closed loop system with cascade controller, in Matlab.

I use program which is given by teacher, but the last figure still wrong? I want to know wheres wrong.

This is the program:

%Part B

%For initial 'K'

%max %OS = 2%, peak time Tp = 0.3, 0% steady state error

%Transfer function

s = tf('s');

G1 = (s+1)/(s^3 + (20*s^2)+ (105*s) + 120)

P=pole(G1)

Z=zero(G1)

%unit step input

figure(1)

step(G1)

title('System with no PID Controller')

%Damping (Calculated from Nise, equation 4.38, page180)

zeta =0.7797 ;

%Root locus

figure(2)

rlocus(G1)

sgrid(zeta, 0)

% From root locus figure pole is -9.33 +j11.6 and gain K1 = 131

%PROPORTIONAL CONTROL ONLY

% gain

K1 = 65.2

%Feedback with unity feedback

M1=feedback(K1*G1,1)

figure(3)

step(M1)

title('System with P Controller')

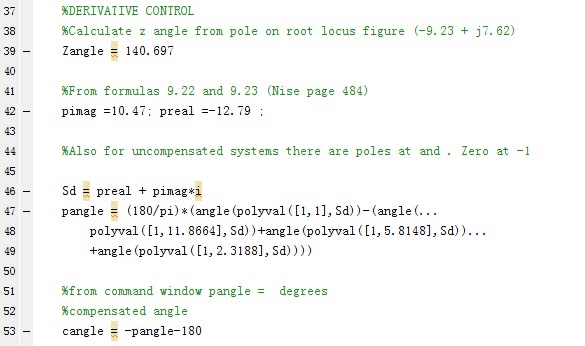
%DERIVATIVE CONTROL

%Calculate z angle from pole on root locus figure (-9.23 + j7.62)

Zangle = 140.697

%From formulas 9.22 and 9.23 (Nise page 484)

pimag =10.47; preal =-12.79 ;

%Also for uncompensated systems there are poles at and . Zero at -1

Sd = preal + pimag*i

pangle = (180/pi)*(angle(polyval([1,1],Sd))-(angle(...

polyval([1,11.8664],Sd))+angle(polyval([1,5.8148],Sd))...

+angle(polyval([1,2.3188],Sd))))

%from command window pangle = degrees

%compensated angle

cangle = -pangle-180

zc = (pimag/tand(cangle))- preal

%from command window zc =

%Giving D Controller Gd(s) = (s + )

Gd = tf([1 zc],[1])

%We need a new K(P) value for PD controller so to find this calculate

%new transfer function Gd*G1

G2 = series(Gd,G1)

%Plot the rlocus of combined open loop transfer function

figure(4)

rlocus(G2) % plot open loop rlocus

sgrid(zeta,0) %include damping factor lines

%15. Measure gain at intersection with zeta line K2 = in this case.

%K2*G2(s) into closed loop transfer function with unity feedback

K2 =23.8;

M2=feedback(K2*G2,1)

%Plot step response to check response

figure(5)

step(M2) %the step response of the compensated closed loop system

%Include integral controller

Gi = tf([1 0.5],[1 0])

G3 = series(Gi,G2)

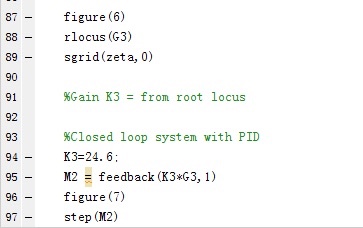
%Root locus of compensated system

figure(6)

rlocus(G3)

sgrid(zeta,0)

%Gain K3 = from root locus

%Closed loop system with PID

K3=24.6;

M2 = feedback(K3*G3,1)

figure(7)

step(M2)

%For initial ,K, %max %OS = 2%, peak time Ip = 0.3, 0% steady state error Iransfer function s = GI 7 tf (' s' ) ; - 8 (s+1 ) / (s^3 + (20*s^2)+ (105*s) + 120) - 10-Ppole (G1) 11ZEzero (G1) 12 13 %unit st ep input 14figure (1) 15step (G1) 16-title( System with no PID Controller)