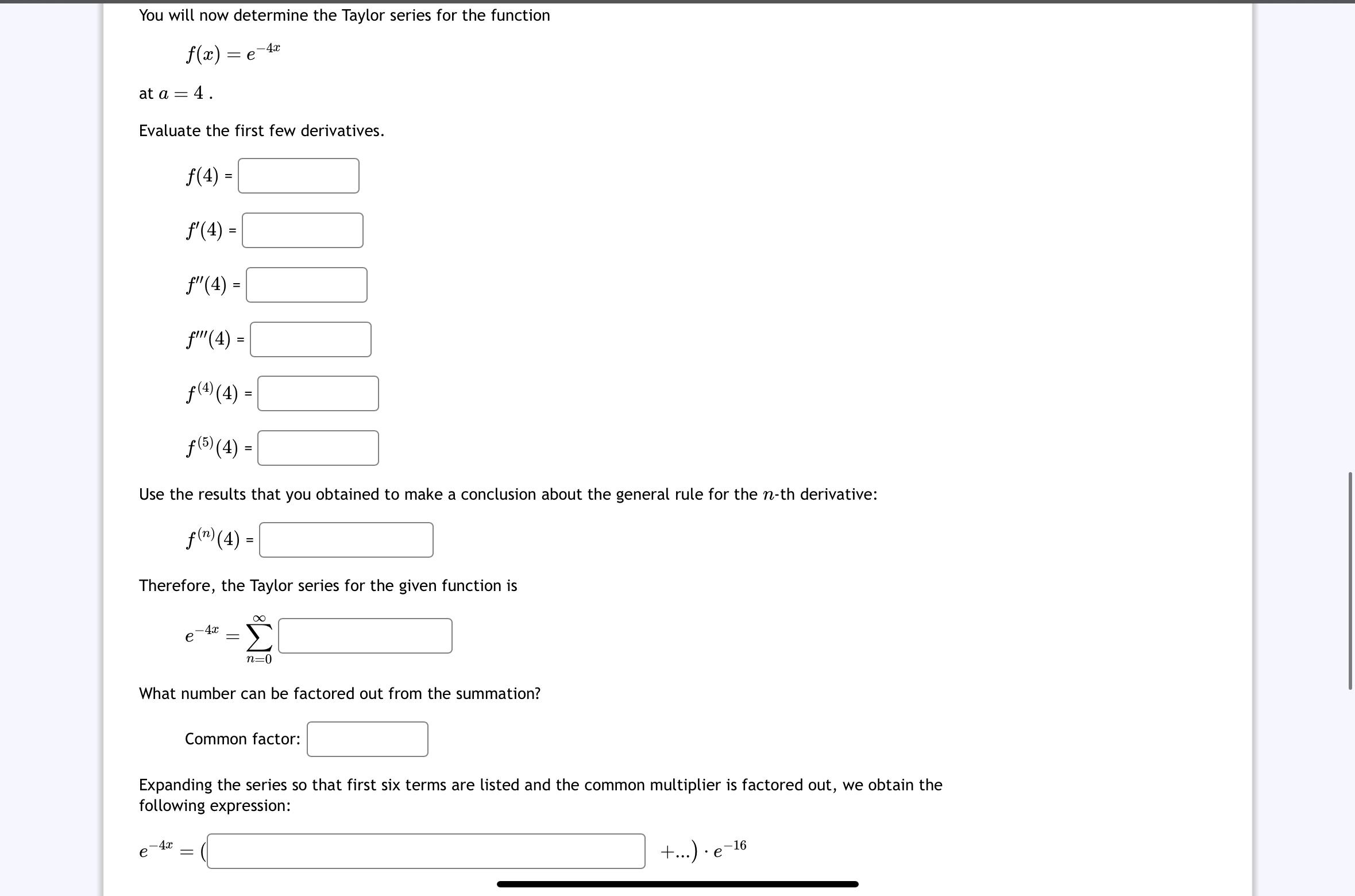
You will now determine the Taylor series for the function

f$($x$)=$e$^(-4$x$)$

at a$=4.$

Evaluate the first few derivatives.

f$(4)=$

f$^(\text{'})(4)=$

f$^(\text{'}\text{'})(4)=$

f$^(\text{'}\text{'}\text{'})(4)=$

f$^((4))(4)=$

f$^((5))(4)=$

Use the results that you obtained to make a conclusion about the general rule for the n$-$th derivative:

f$^(($n$))(4)=$

Therefore, the Taylor series for the given function is

What number can be factored out from the summation?

Common factor:

Expanding the series so that first six terms are listed and the common multiplier is factored out, we obtain the

following