Compare the models that you have found in Problems 10.17, 10.18, and 10.19 by calculating the confidence intervals on the mean of the response PITCH for all points in the original data set. Based on a comparison of these confidence intervals, which model would you prefer? Now calculate the PRESS statistic for these models. Which model would PRESS indicate is likely to be the best for predicting new observations on PITCH?

Data From Problem 10.17

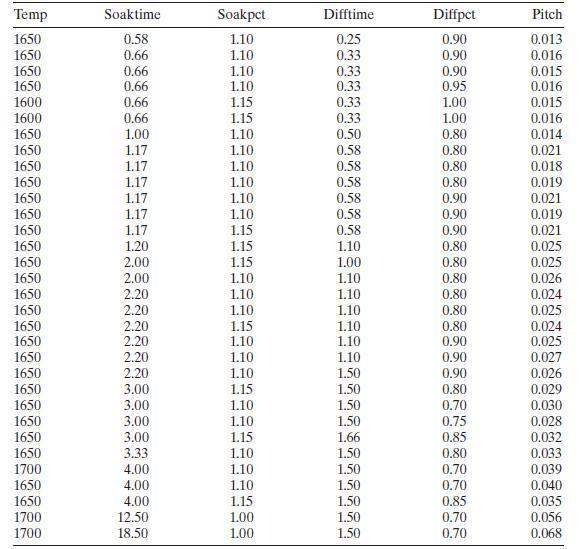
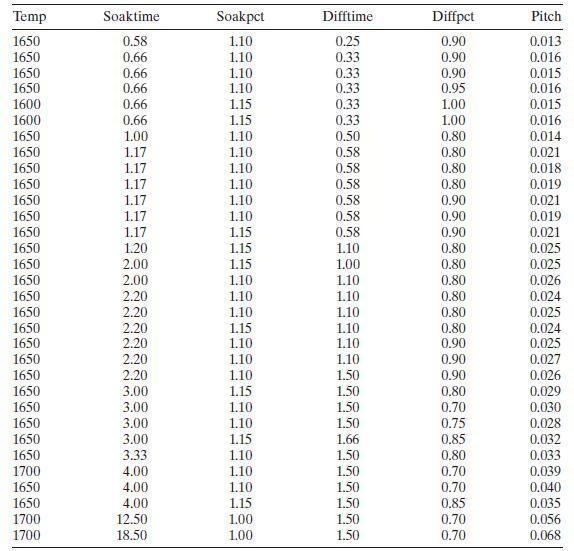
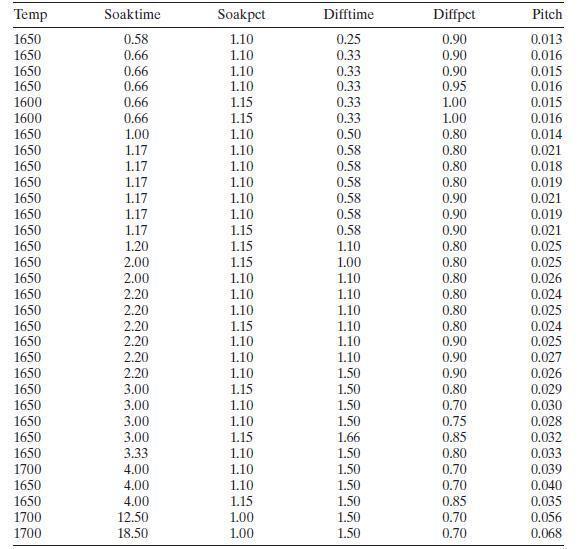
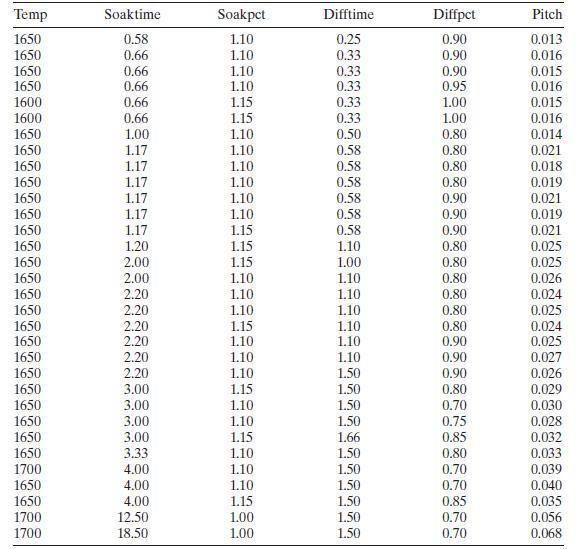
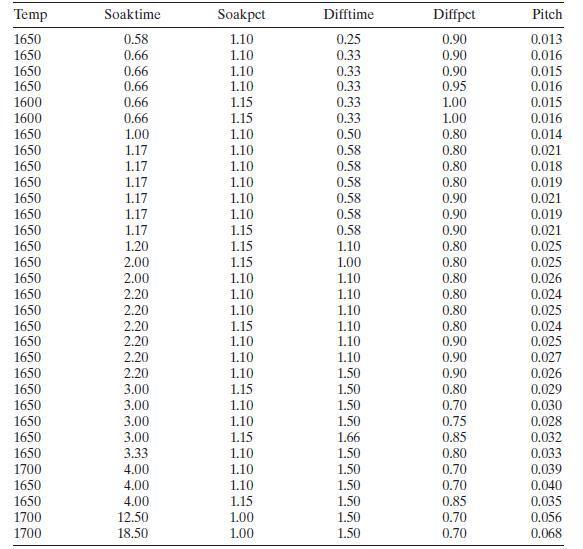
Table B. 12 presents data on a heat treating process used to carburize gears. The thickness of the carburized layer is a critical factor in overall reliability of this component. The response variable y=y=y=$\mathrm{????}=$ PITCH is the result of a carbon analysis on the gear pitch for a cross-sectioned part. Use all possible regressions and the CpCpCp${\mathrm{????}}_{\mathrm{????}}$ criterion to find an appropriate regression model for these data. Investigate model adequacy using residual plots.

Data From Problem 10.18

Reconsider the heat treating data from Table B.12. Fit a model to the PITCH response using the variables

x1=SOAKTIME×SOAKPCT and x2= DIFFTIME × DIFFPCT x1=SOAKTIME×SOAKPCT and x2= DIFFTIME × DIFFPCT ${\mathrm{????}}_1=\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\times \mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\text{ and }{\mathrm{????}}_2=\text{ DIFFTIME }\times \text{ DIFFPCT }$
as regressors. How does this model compare to the one you found by the all-possible-regressions approach of Problem 10.17?

Problem 10.17

Table B. 12 presents data on a heat treating process used to carburize gears. The thickness of the carburized layer is a critical factor in overall reliability of this component. The response variable y=y=y=$\mathrm{????}=$ PITCH is the result of a carbon analysis on the gear pitch for a cross-sectioned part. Use all possible regressions and the CpCpCp${\mathrm{????}}_{\mathrm{????}}$ criterion to find an appropriate regression model for these data. Investigate model adequacy using residual plots.

Data Form Problem 10.19

Repeat Problem 10.17 using the two cross-product variables defined in Problem 10.18 as additional candidate regressors. Comment on the model that you find.

Data From Problem 10.17

Table B. 12 presents data on a heat treating process used to carburize gears. The thickness of the carburized layer is a critical factor in overall reliability of this component. The response variable y=y=$\mathrm{????}=$ PITCH is the result of a carbon analysis on the gear pitch for a cross-sectioned part. Use all possible regressions and the CpCp${\mathrm{????}}_{\mathrm{????}}$ criterion to find an appropriate regression model for these data. Investigate model adequacy using residual plots.

Data From Problem 18

Reconsider the heat treating data from Table B.12. Fit a model to the PITCH response using the variables

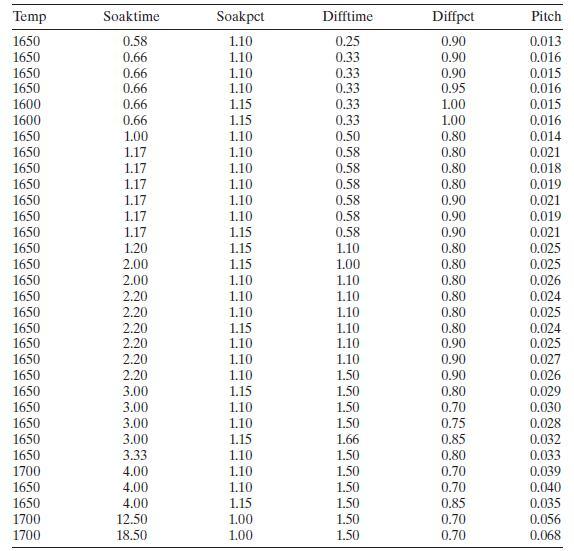
x1=SOAKTIME×SOAKPCT and x2= DIFFTIME × DIFFPCT ${\mathrm{????}}_1=\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\times \mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\mathrm{????}\text{ and }{\mathrm{????}}_2=\text{ DIFFTIME }\times \text{ DIFFPCT }$
as regressors. How does this model compare to the one you found by the all-possible-regressions approach of Problem 10.17?

Problem 10.17

Table B. 12 presents data on a heat treating process used to carburize gears. The thickness of the carburized layer is a critical factor in overall reliability of this component. The response variable y=y=$\mathrm{????}=$ PITCH is the result of a carbon analysis on the gear pitch for a cross-sectioned part. Use all possible regressions and the CpCp${\mathrm{????}}_{\mathrm{????}}$ criterion to find an appropriate regression model for these data. Investigate model adequacy using residual plots.

Temp Soaktime Soakpct Difftime Diffpct Pitch 1650 0.58 1.10 0.25 0.90 0.013 1650 0.66 1.10 0.33 0.90 0.016 1650 0.66 1.10 0.33 0.90 0.015 1650 0.66 1.10 0.33 0.95 0.016 1600 0.66 1.15 0.33 1.00 0.015 1600 0.66 1.15 0.33 1.00 0.016 1650 1.00 1.10 0.50 0.80 0.014 1650 1.17 1.10 0.58 0.80 0.021 1650 1.17 1.10 0.58 0.80 0.018 1650 1.17 1.10 0.58 0.80 0.019 1650 1.17 1.10 0.58 0.90 0.021 1650 1.17 1.10 0.58 0.90 0.019 1650 1.17 1.15 0.58 0.90 0.021 1650 1.20 1.15 1.10 0.80 0.025 1650 2.00 1.15 1.00 0.80 0.025 1650 2.00 1.10 1.10 0.80 0.026 1650 2.20 1.10 1.10 0.80 0.024 1650 2.20 1.10 1.10 0.80 0.025 1650 2.20 1.15 1.10 0.80 0.024 1650 2.20 1.10 1.10 0.90 0.025 1650 2.20 1.10 1.10 0.90 0.027 1650 2.20 1.10 1.50 0.90 0.026 1650 3.00 1.15 1.50 0.80 0.029 1650 3.00 1.10 1.50 0.70 0.030 1650 3.00 1.10 1.50 0.75 0.028 1650 3.00 1.15 1.66 0.85 0.032 1650 3.33 1.10 1.50 0.80 0.033 1700 4.00 1.10 1.50 0.70 0.039 1650 4.00 1.10 1.50 0.70 0.040 1650 4.00 1.15 1.50 0.85 0.035 1700 12.50 1.00 1.50 0.70 0.056 1700 18.50 1.00 1.50 0.70 0.068