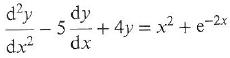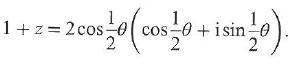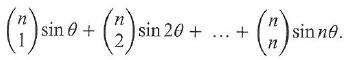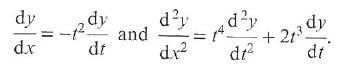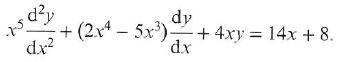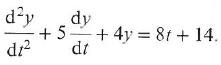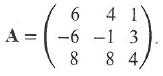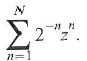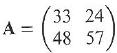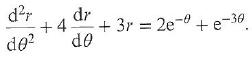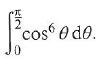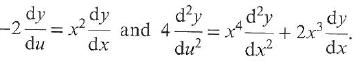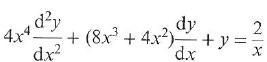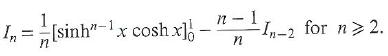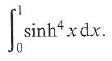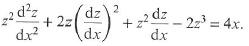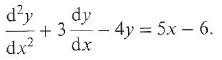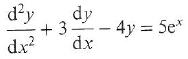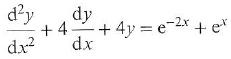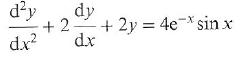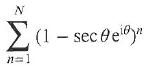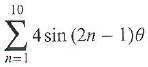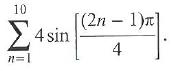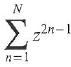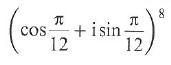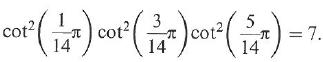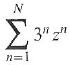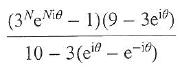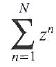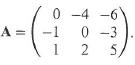Cambridge International AS & A Level Further Mathematics Coursebook 1st Edition Lee Mckelvey, Martin Crozier - Solutions

Discover comprehensive solutions to the challenging problems in the "Cambridge International AS & A Level Further Mathematics Coursebook 1st Edition" by Lee Mckelvey and Martin Crozier. Our online platform provides an extensive answers key with detailed solutions, including a solution manual and solutions in PDF format. Benefit from solved problems, questions and answers, and a robust test bank to enhance your understanding. Explore chapter solutions and step-by-step answers that cater to every mathematical inquiry. With our instructor manual, this textbook becomes an invaluable resource. Enjoy the convenience of free download options for all educational materials.