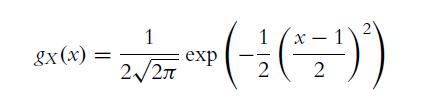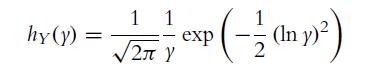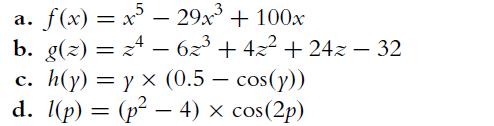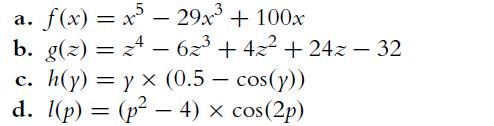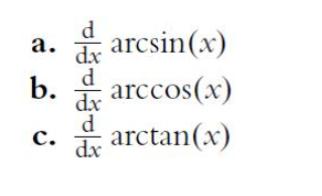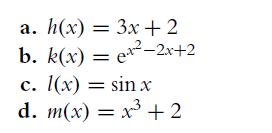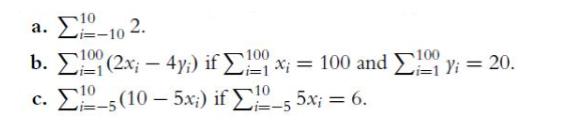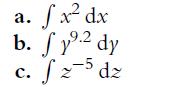![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



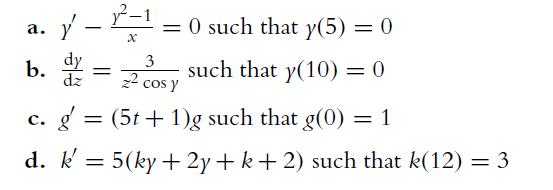
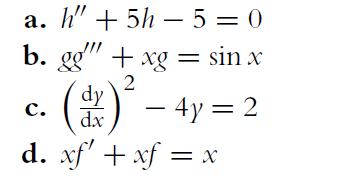
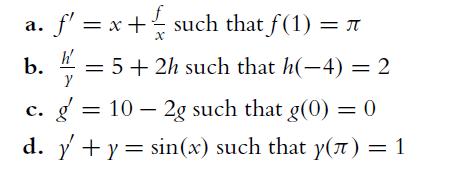
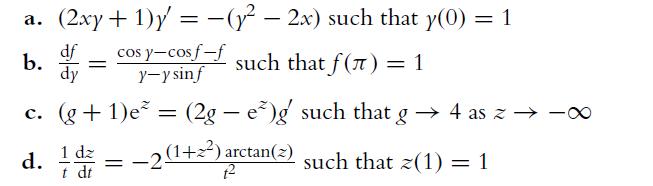
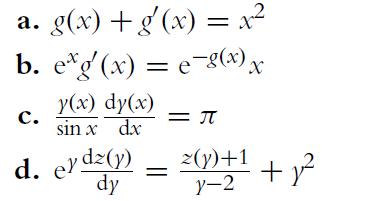
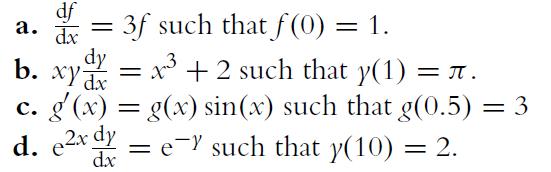
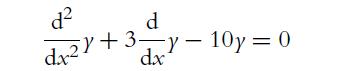
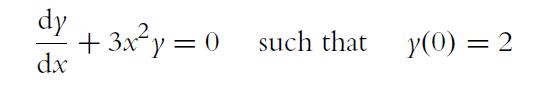

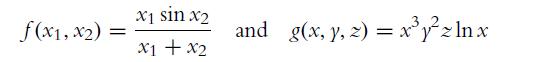
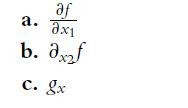
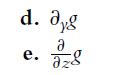
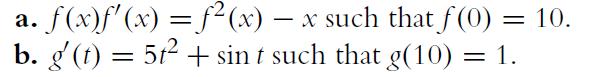
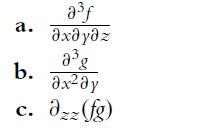

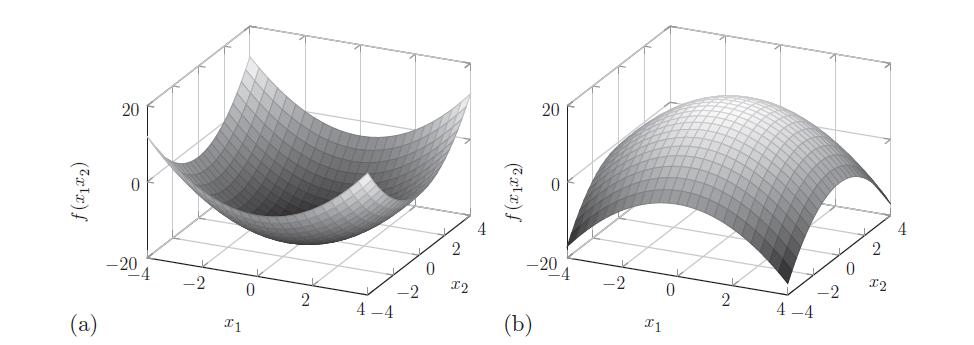
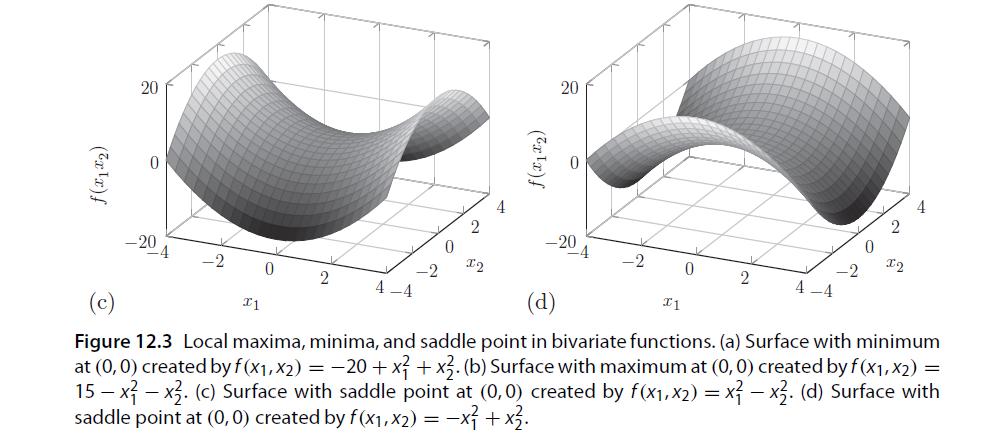
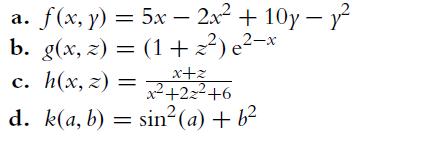
![a. ff 2xy dx dy for Da = {x,ylx = [1, 2], y [2, 4]}. Da b. C. ff(x+ 10) dx dz for D = {x, zx [0, 10], z =](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/1/6/65465743d2ea6abc1702116652540.jpg)
![ff 2xy dx dy for Da = {x, y]x = [1, 2], y = [-x, x]}. Da b. ff(x+ 10) dx dz for Db = {x, z|x [2z, 4z], z](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/1/6/67365743d416c54f1702116671529.jpg)

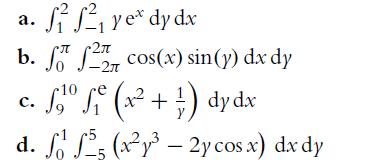
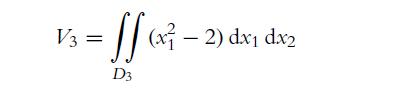

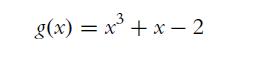
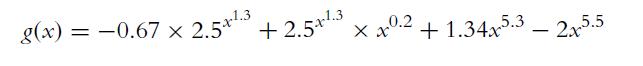
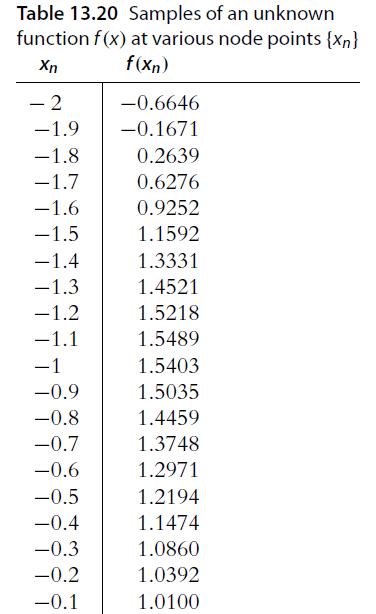

![a. [a, b] = [0, 2] b. [a, b] = [-4, -2] C. [a, b] = [0, 2]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/1/7/9636574424bdbe621702117959463.jpg)
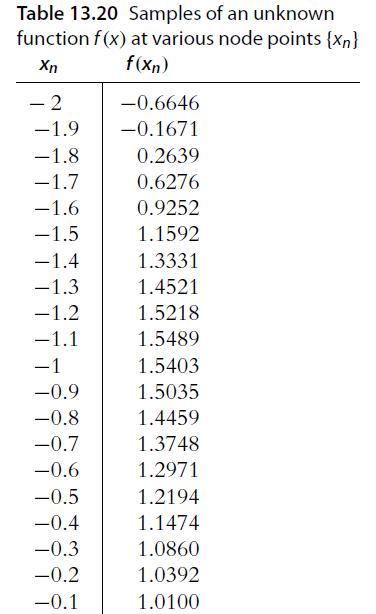

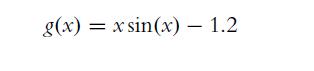
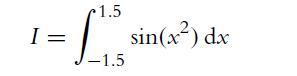
![fs(s) $200 = - exp 1 (In(s) - 1) 2 0.2 2 for s [0.1,6.1]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/3/5/3746574864e2b2a31702135372182.jpg)
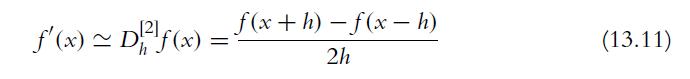
![[2] f'(x) ~ Df(x): h = f(x+h)-f(xh) 2h (13.11)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/1/8/7026574452e13d9a1702118698927.jpg)
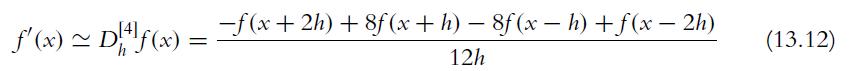
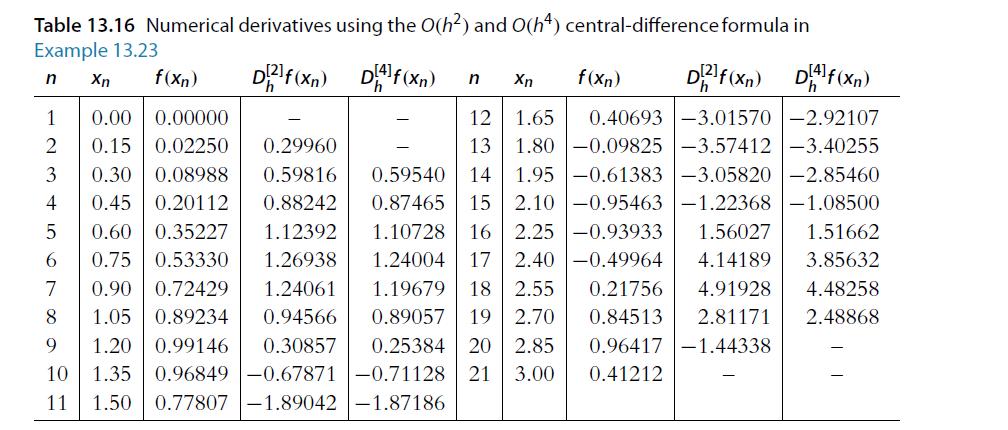
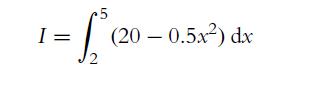
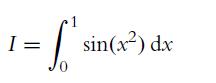
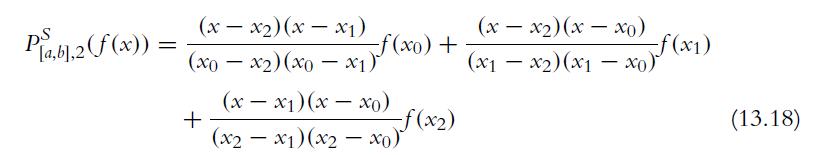
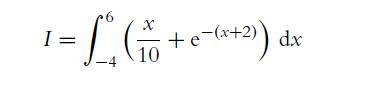
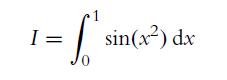
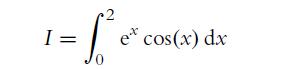
![a. fx(x) = sin(x) for x = [-, 00]. b. gy(y) = for y [a, b] and b> a are real constants. c. hz(2) = ez for z](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/3/4/502657482e642f2f1702134500121.jpg)
![fx (x) = a sin(x) for x = [0,5]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1702/1/3/4/513657482f1564f01702134511280.jpg)