Consider the complex function x(t) = (1 + jt)² for − ∞ < t < ∞.

(a) Find the real and the imaginary parts of x(t) and carefully plot them with MATLAB. Try to make MATLAB plot x(t) directly, what do you get? Does MATLAB warn you? Does it make sense?.

(b) Compute the derivative y(t) = dx(t)/dt and plot its real and imaginary parts, how do these relate to the real and the imaginary parts of x(t)?

(c) Compute the integral

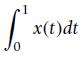
(d) Would the following statement be true? (remember *indicates complex conjugate)

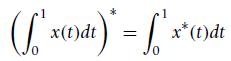
x(t)dt