Suppose you want to design a dc-source using a half-wave rectified signal x(t) and an ideal filter. Let x(t) be periodic, T₀= 2, and with a period

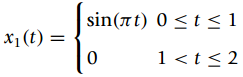
(a) Find the Fourier transform X(Ω) of x(t), and plot the magnitude spectrum including the dc and the first three harmonics.

(b) Determine the magnitude and cut-off frequency of an ideal low-pass filter H(jΩ)such that when we have x(t) as its input, the output is y(t) = 1. Plot the magnitude response of the ideal low-pass filter. (For simplicity assume the phase is zero).

sin(ët) 0 < t <1 x1 (t) = 1